om which a small circular piece of radius b << a has been removed. What is the direction and magnitude of the
Q: Imagine that two parallel plates are charged to achieve a voltage difference Vo between the plates.…
A: Given:Initial voltage difference between the plate = V0Distance between the plates = dPlate area = A
Q: The volume charge density of a spherically charged cloud changes with the distance to the cloud…
A:
Q: In a cathode-ray tube (CRT), an electron travels in a vacuum and enters a region between two…
A: Length of plate L= 0.12 m Breadth of plate d= 0.05 m Distance between plates h= 2.5×10-3 m Time…
Q: a) Find the surface charge density σ2 of the cylindrical shell of radius R2. (Note the unit in the…
A: (a). As given the cable as a whole is neutral, Thus, the charge on the inner cable and outer cable…
Q: Imagine that two parallel plates are charged to achieve a voltage difference Vo between the plates.…
A: Given:Initial voltage difference between the plate = V0Distance between the plates = dPlate area = A
Q: Two thin concentric spherical shells of radii r1 and r2 (ri r2. Neglect the thickness of the…
A: Two thin spherical shells of radii,, and surface densities are, respectively. The arrangement of the…
Q: A point charge + Q is placed at the centre of an uncharged spherical conducting shell of inner…
A: By using gauss law we can solve all three parts easily.
Q: Figure 1.52 shows a spherical shell of charge, of radius a and surface density σ, from which a small…
A: The electric field for charged spherical shell or conductor is given by, The field outside, Eout=σε0…
Q: A solid conducting sphere carrying charge q has radius a. It is inside a concentric hollow…
A:
Q: Problem 1.2.3. Three particles with equal positive charge q are at the corners of a square of side…
A: Three particles with equal positive charge q are at corners of square of side 'd'.(a). The fourth…
Q: Charge is distributed throughout a spherical volume of radius R with a density p= ar², where a is a…
A: Given that: Charge density, ρ=αr2
Q: Problem 2: A closed hollow cylinder (i.e., with capped ends) is situated in an electric field…
A:
Q: Please don't provide handwritten solution .....
A: From the figure , range of x is from 0 to 4 range of y is also from 0…
Q: YouD're 1.44 m from a charge distribution that is well under 1 cm in size. You measure an electric…
A:
Q: What would be the electric field for z0 > R for the following integral? The integral is the answer…
A:
Q: Charge is distributed throughout a spherical shell of inner radius ₁ and outer radius r2 with a…
A:
Q: Let F(x, y, z) = x ₁²+yẩy + záz be a vecter field. хакту чату a- Express F in cylindrical and…
A:
Q: An infinitely long insulating cylinder of radius R=1.2m has a volume charge density that varies with…
A:
Q: A point charge +Q is placed at the centre of an uncharged spherical conducting shell of inner radius…
A:
Q: Using the method of integration, what is the electric field of a uniformly charged thin circular…
A: Given Using the method of integration, what is the electric field of a uniformly charged thin…
Q: I need help on this? Could you write an explanation on how you came up with the answers
A: The objective of this question is to understand how the variables in Coulomb's Law interact with…
Q: A 2D annulus (thick ring) has an inner radius Ri and outer radius Ro, and charge Q non-uniformly…
A:
Q: Problem An insulating sphere with radius R contains a total non-uniform charge (i.e. Hydrogen atom)…
A: Gauss's law states that the total electric flux through a closed surface is given by the ratio of…
Q: Two oppositely charged but otherwise identical conducting plates of area 2.50 square centimeters are…
A: In this problem, it is asking to solve for sub-part (c) only. Therefore, we will solve the sub-part…
Q: Compute the flux of the vector field F = 2zk through S, the upper hemisphere of radius 6 centered at…
A:
Q: Evaluate the line integral, where C is the given curve. Sc (x + yz)dx + 2x dy + xyz dz C consists of…
A: Disclaimer- As your given image contains multiple questions, following the guide-lines we will only…
Q: An insulating solid sphere of radius 3 m has 15 C of charge uniformly distributed throughout its…
A: Let us consider the gaussian surface which have a radius which is half the radius of the insulating…
Figure 1.52 shows a spherical shell of charge, of radius
a and surface density σ, from which a small circular piece of radius b << a has been removed. What is the direction and magnitude of the field at the midpoint of the aperture? Solve this exercise using direct integration.
Electric field at the center of integrated charged sphere is zero so when we remove the disc shaped portion, there will develop an electric field at the center of remaining aperture which will be equal in magnitude to the electric field of the disc at its axis at a distance equal to radius of sphere and opposite in direction.
Charge density =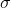 
, radius of disc = b, distance over the axis = R.
Step by step
Solved in 2 steps with 1 images
- Problem 2.01. Three plates with surface charge density |o| = 8.85 μC/mm² are stacked on top of each other. The top and bottom plates have charge density to while the center plate has charge density -0. (a) Find the magnitude and direction of the electric field between the plates. (b) Find the magnitude and direction of the electric field above and below the plate stack.2.6The classic Millikan oil drop experiment was the first to obtain an accurate measurement of the charge on an electron. In it, oil drops were suspended against the gravitational force by a vertical electric field. 1a. Given the oil drop to be 0.99 μm in radius and have a density of 910 kg/m3: Find the weight of the drop. 1b.If the drop has a single excess electron, find the electric field strength needed to balance its weight. This is not and will not be graded
- Consider an infinitely long wire of charge carrying a positive charge density of A. The electric field due to λ this line of charge is given by E= 2kef= -, where is a unit vector directed radially outward Σπερμ from the infinitely long wire of charge. Hint #3 a. Letting the voltage be zero at some reference distance (V(ro) = 0), calculate the voltage due to this infinite line of charge at some distance r from the line of charge. Give your answer in terms of given quantities (A,ro,r) and physical constants (ke or Eo). Use underscore ("_") for subscripts and spell out Greek letters. Hint for V(r) calculation 3 V(r) = b. There is a reason we are not setting V(r → ∞o) = 0 as we normally do (in fact, in general, whenever you have an infinite charge distribution, this "universal reference" does not work; you need a localized charge distribution for this reference to work). Which of the following best describes what happens to potential as roo? (That is, what is V(ro), with our current…None2.1. Four 10nC positive charges are located in the z = 0 plane at the corners of a square 8cm on a side. A fifth 10nC positive charge is located at a point 8cm distant from the other charges. Calculate the magnitude of the total force on this fifth charge for e = €0: Arrange the charges in the xy plane at locations (4,4), (4,-4), (-4.4), and (-4,-4). Then the fifth charge will be on the z axis at location z = 4/2, which puts it at 8cm distance from the other four. By symmetry, the force on the fifth charge will be z-directed, and will be four times the z component of force produced by each of the four other charges.