objective: Show that IZ is irrational Proof by contradiction: Assume tz is rational: which means it can be expressed as to where b‡, and there is no common factors between and to So, √√√2 = 10 9 2/6²³-a³ Since a³ is equal to 26³, and 26³ must even integer, since any positive inteover musipried - 6Y 2 is even. a³ must be even, be an since a a*a*a, and a³ is even. a must be even as well. So a =2k, where KEZ => 26³ = (24) 263 = 8k³ 6²³ = 4K³ Since any integer, not 0, multiplied by an even number results in an even number. 16 must be even since both 6 and a are even Share band a a common factor of 2 Therefore, is irrational by contradiction GED
objective: Show that IZ is irrational Proof by contradiction: Assume tz is rational: which means it can be expressed as to where b‡, and there is no common factors between and to So, √√√2 = 10 9 2/6²³-a³ Since a³ is equal to 26³, and 26³ must even integer, since any positive inteover musipried - 6Y 2 is even. a³ must be even, be an since a a*a*a, and a³ is even. a must be even as well. So a =2k, where KEZ => 26³ = (24) 263 = 8k³ 6²³ = 4K³ Since any integer, not 0, multiplied by an even number results in an even number. 16 must be even since both 6 and a are even Share band a a common factor of 2 Therefore, is irrational by contradiction GED
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Did I prove this well?

Transcribed Image Text:objective: Show that IZ is irrational
Proof by contradiction:
Assume = is rational: which means it can be
expressed as to where b#, and there is
factors between
and to
no commen
So, √√√2 = 16
120
-10³
2/0²³-a³
Since a
is equal to 26³, and 26³ must
even integer, since any positive intover multiplied
- 6Y 2 is even. a³ must be even,
be an
since d
a*a*a, and a³ is even.
a must be even
as well. So a = 2K, where KEZ
=> 26³ =
(24)
263
= 8k³
6²³ = 4K³
Since any integer, not of multiplied by an
even number
results in an even number.
16 must be even
since both 6 and a are even
Share
band
a
a common factor of 2
Therefore, is irrational by contradiction
GED
Expert Solution
Step 1: Explaining the question.
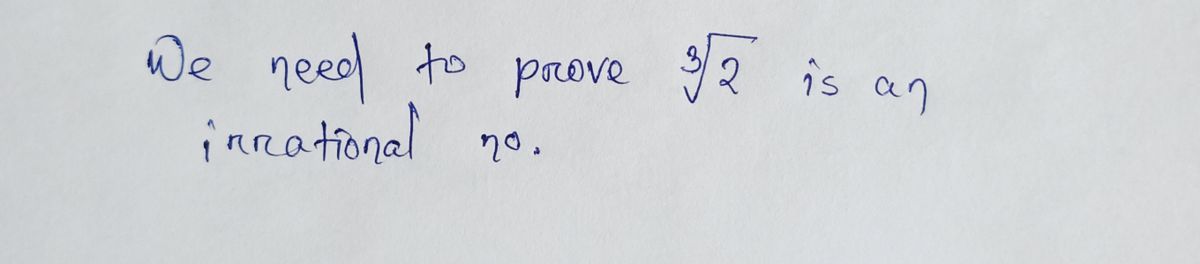
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

