Objective #4: Solve problems involving the relationship between a central angle of a circle and the length of its intercepted arc 1. Find the length of the arc on a circle of radius r = 15 inches intercepted by a central angle 0 = 120°. 2. Find the radian measure of the central angle of a circle of radius r = 80 kilometers that intercepts an arc of length s = 150 kilometers. 3. Use the given arc length and radius to find angle 0 (in radians). 28 8 7
Objective #4: Solve problems involving the relationship between a central angle of a circle and the length of its intercepted arc 1. Find the length of the arc on a circle of radius r = 15 inches intercepted by a central angle 0 = 120°. 2. Find the radian measure of the central angle of a circle of radius r = 80 kilometers that intercepts an arc of length s = 150 kilometers. 3. Use the given arc length and radius to find angle 0 (in radians). 28 8 7
Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.CT: Test
Problem 1CT
Related questions
Question
![### Educational Text on Trigonometry in Real-Life Applications
#### 3. Empire State Building
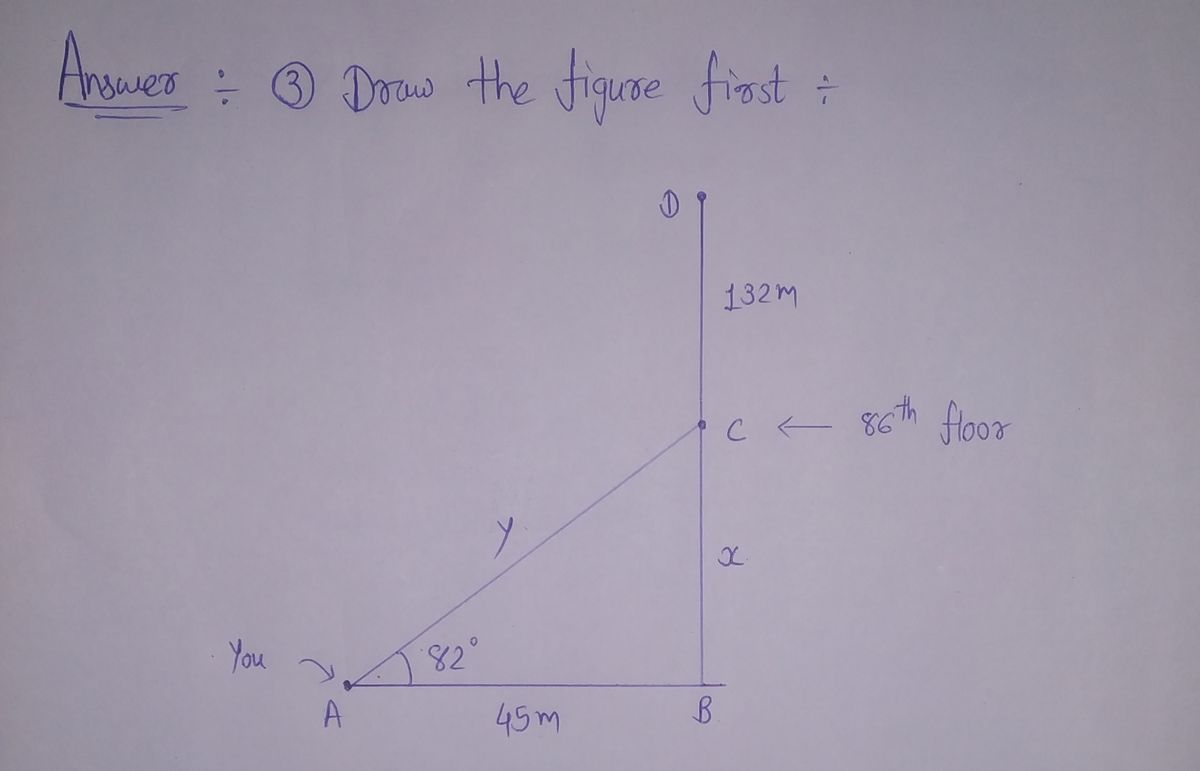
You are standing 45 meters from the base of the Empire State Building. You estimate that the angle of elevation to the top of the 86th floor (the observatory) is 82°. The total height of the building is another 132 meters above the 86th floor. What is the approximate height of the building? One of your friends is on the 86th floor. What is the distance between you and your friend?
---
#### 4. Length
A guy wire runs from the ground to a cell tower. The wire is attached to the cell tower 150 feet above the ground. The angle formed between the wire and the ground is 43° (see figure).
**Diagram Description:**
The diagram illustrates a right triangle where the tower represents the vertical side (opposite angle θ), the ground represents the horizontal side (adjacent to angle θ), and the guy wire represents the hypotenuse.
- **Vertical Side (Height of Tower):** 150 feet
- **Angle (θ):** 43°
**Questions:**
(a) **How long is the guy wire?**
To find the length of the guy wire (hypotenuse), use the sine function:
\[ \sin(43°) = \frac{150}{\text{guy wire}} \]
(b) **How far from the base of the tower is the guy wire anchored to the ground?**
To find the distance from the base of the tower to the point where the wire is anchored (adjacent side), use the tangent function:
\[ \tan(43°) = \frac{150}{\text{base distance}} \]
---
This exercise demonstrates the application of trigonometric functions such as sine and tangent in calculating distances and lengths in real-world scenarios.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F513aadd7-c916-4179-86cd-11c0f7eed57f%2F29f64115-2ee5-4fc8-ac84-a8220ab829d0%2F4tv2ekj_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Educational Text on Trigonometry in Real-Life Applications
#### 3. Empire State Building
You are standing 45 meters from the base of the Empire State Building. You estimate that the angle of elevation to the top of the 86th floor (the observatory) is 82°. The total height of the building is another 132 meters above the 86th floor. What is the approximate height of the building? One of your friends is on the 86th floor. What is the distance between you and your friend?
---
#### 4. Length
A guy wire runs from the ground to a cell tower. The wire is attached to the cell tower 150 feet above the ground. The angle formed between the wire and the ground is 43° (see figure).
**Diagram Description:**
The diagram illustrates a right triangle where the tower represents the vertical side (opposite angle θ), the ground represents the horizontal side (adjacent to angle θ), and the guy wire represents the hypotenuse.
- **Vertical Side (Height of Tower):** 150 feet
- **Angle (θ):** 43°
**Questions:**
(a) **How long is the guy wire?**
To find the length of the guy wire (hypotenuse), use the sine function:
\[ \sin(43°) = \frac{150}{\text{guy wire}} \]
(b) **How far from the base of the tower is the guy wire anchored to the ground?**
To find the distance from the base of the tower to the point where the wire is anchored (adjacent side), use the tangent function:
\[ \tan(43°) = \frac{150}{\text{base distance}} \]
---
This exercise demonstrates the application of trigonometric functions such as sine and tangent in calculating distances and lengths in real-world scenarios.

Transcribed Image Text:**Objective #4: Solving Problems Involving the Relationship Between a Central Angle of a Circle and the Length of Its Intercepted Arc**
1. Find the length of the arc on a circle of radius \( r = 15 \) inches intercepted by a central angle \( \theta = 120^\circ \).
2. Find the radian measure of the central angle of a circle of radius \( r = 80 \) kilometers that intercepts an arc of length \( s = 150 \) kilometers.
3. Use the given arc length and radius to find angle \( \theta \) (in radians).
---
**Diagram Explanation:**
A diagram of a circle is shown. The circle has a marked radius of 7 and a larger radius of 28. An angle \( \theta \) is depicted at the center, subtending an arc on the circle.
Expert Solution
Step 1a
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning