Now that we have practiced finding the Characteristic Solution, we can determine our Assumed Particular Solution. The Assumed Particular Solution is always an Exact Copy of the Characteristic Solution but with the C and C2 with u, and uz. -3x Charcateristic Solution y (x) = C, e* + C, e Sx e Sx + 4, e -3x Particular Solution y,(x) = The benefit of this method is that we will only every have exactly 4" + C's " to find; no mater how complicated the differential equation is. The down side is that these "+C's" can become very complicated and will probably include variables. Hence the name "variation of parameters", or stated in another way, "coefficients with variables". Given the characteristic solution e(x) = C, cos(2x) + C, sin(2r) Set up your Particular Solution, then use it to determine your y, and y2, finally find the value of the Wronskian using the following formula. W = y,y2' - y,'Y2 A W = 2 sin(4x) W = 2 cos?(2x) – 2 sin²(2x) W = 4 cos(2x) sin(2x) D W = 2 E W = 2 cos2(2x) + 2 sin?(2x) B.
Now that we have practiced finding the Characteristic Solution, we can determine our Assumed Particular Solution. The Assumed Particular Solution is always an Exact Copy of the Characteristic Solution but with the C and C2 with u, and uz. -3x Charcateristic Solution y (x) = C, e* + C, e Sx e Sx + 4, e -3x Particular Solution y,(x) = The benefit of this method is that we will only every have exactly 4" + C's " to find; no mater how complicated the differential equation is. The down side is that these "+C's" can become very complicated and will probably include variables. Hence the name "variation of parameters", or stated in another way, "coefficients with variables". Given the characteristic solution e(x) = C, cos(2x) + C, sin(2r) Set up your Particular Solution, then use it to determine your y, and y2, finally find the value of the Wronskian using the following formula. W = y,y2' - y,'Y2 A W = 2 sin(4x) W = 2 cos?(2x) – 2 sin²(2x) W = 4 cos(2x) sin(2x) D W = 2 E W = 2 cos2(2x) + 2 sin?(2x) B.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
q4

Transcribed Image Text:Now that we have practiced finding the Characteristic Solution, we can determine our Assumed Particular Solution. The Assumed
Particular Solution is always an Exact Copy of the Characteristic Solution but with the C and C2 with u, and uz.
Charcateristic Solution y (x) = C, e* + C, e
Sx
Particular Solution y,(x) =
e Sx
+ H,e
The benefit of this method is that we will only every have exactly 4" + C's " to find; no mater how complicated the differential
equation is. The down side is that these "+C's" can become very complicated and will probably include variables. Hence the name
"variation of parameters", or stated in another way, "coefficients with variables".
Given the characteristic solution
Ye(x) = C, cos(2x) + C, sin(2x)
Set up your Particular Solution, then use it to determine your y, and y2 finally find the value of the Wronskian using the following
formula.
W = y,y2' - y,'Y2
A
W = 2 sin(4x)
W = 2 cos?(2x) – 2 sin²(2x)
W = 4 cos(2x) sin(2x)
D
W = 2
E
W = 2 cos2(2x) + 2 sin?(2x)
B.
Expert Solution
Step 1
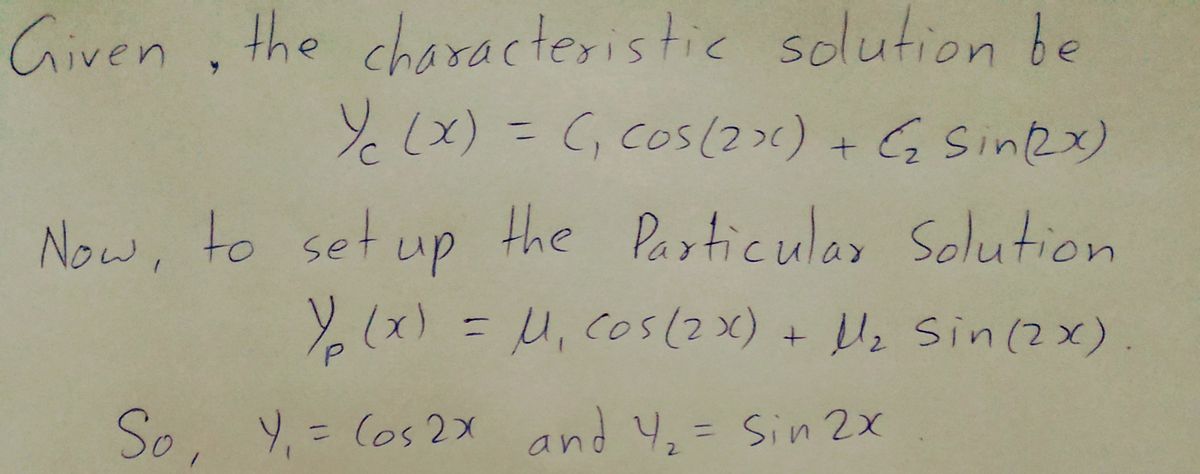
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

