Problem 5.6 Use Parseval's identity to evaluate the following integrals: sinc(2t - 3)sinc(3t+1)dt (a) (b) o sinc¹(5t)dt.
Problem 5.6 Use Parseval's identity to evaluate the following integrals: sinc(2t - 3)sinc(3t+1)dt (a) (b) o sinc¹(5t)dt.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Use Parseval’s identity to evaluate the following
(a) R ∞ −∞ sinc(2t + 1)sinc(3t − 1)dt
(b) R ∞ 0 sinc4 (3t)dt. please have a step by step solution and explain. I need to know how to approach the problem

Transcribed Image Text:Problem 5.6 Use Parseval's identity to evaluate the following integrals:
(a) sinc(2t - 3)sinc(3t+1)dt
(b) sinc¹(5t)dt.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 10 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
you did part a wrong. shouldnt there be 2 shifts? what happened to the shift from sin(3t+1)? why is it not included in the
![a)
sinc(2t-3) sinc(3t+1)dt
Let | =
The Parseval's identity:
=
sinc(2t-3)sinc(3t+1)dt
-∞0
-∞
Where G(s) = Fourier transform's
F(s)G(s)ds
f(t)g (t) = F(s)G(s)ds
=
S
|=
Xπ
50 [17 (2)] 0-10/31 x 1
e-ls/31,
³1×××
1
[²²/1 × ² / ×
-1
2
3
e ds
1 = 1/361/60
S
+1
-3e
-|s/31
X xe
1=[1-e-³]
53-|ds](https://content.bartleby.com/qna-images/question/9b42e249-3ec9-4b52-9315-d0264313923a/abf3216c-252f-4f20-8d5d-00626599b634/1tmu91_thumbnail.png)
Transcribed Image Text:a)
sinc(2t-3) sinc(3t+1)dt
Let | =
The Parseval's identity:
=
sinc(2t-3)sinc(3t+1)dt
-∞0
-∞
Where G(s) = Fourier transform's
F(s)G(s)ds
f(t)g (t) = F(s)G(s)ds
=
S
|=
Xπ
50 [17 (2)] 0-10/31 x 1
e-ls/31,
³1×××
1
[²²/1 × ² / ×
-1
2
3
e ds
1 = 1/361/60
S
+1
-3e
-|s/31
X xe
1=[1-e-³]
53-|ds
Solution
Follow-up Question
NO i need it to be the Fourier transform as X(jw). Dont use this as s tranfer functions
I dont understand the triangle. where did you get it from? i did not learn it that way. also you didnt explain the change in bounds in the integral. i dont understand how that triangle becomes (s+5). so can you please have a better explanation to this problem? why is f(t) sinc^2 (5t) ? i thought the given function was sinc^4(5t).
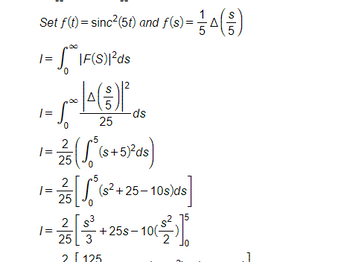
Transcribed Image Text:Set f(t) = sinc2(5t) and f (s) =
= | * IF(S)|ds
1=
0
امام
1=
-ds
- ( *(s+52ds)
2
25
5
25
0
) = (3)
A
5
2
[ * (2 + 25 - 10s)ds
+ |
15
25 0
2 [ 3
1= +255-102²
25 3
2125
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

