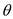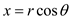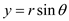n= 2
Consider the polar-coordinate stream function ψ = Br1/2
sin(1.2 θ), with B equal, for convenience, to 1.0 ft0.8/s.
(a) Plot the streamline ψ = 0 in the upper half plane.
(b) Plot the streamline ψ = 1.0 and interpret the fl ow
pattern. (c) Find the locus of points above ψ = 0 for which
the resultant velocity = 1.2 ft/s.
(a)
Write the streamline equation in polar coordinate.
Substitute 0 for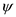 
.
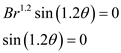
The sin value of a quantity can be zero only when the quantity is equal to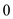 
and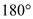 
.
So,
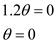
And,
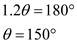
This is the case of a potential flow around a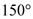 
corner.
So, the plot the streamline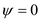 
in the upper half plane as shown in the following figure:
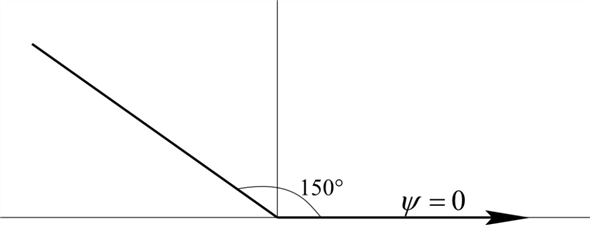
(b)
Consider the streamline at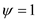 
.
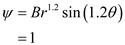
Upon rearranging the terms the equation assumes the following form:
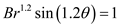
Substitute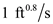 
for B.
Apply logarithms with base e on both sides of the equation.
Calculate the values of r, x, and y for a range of the values of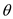 
as follows:
|
(degrees) |
r |
|
|
|
0 |
Not defined |
Not defined |
Not defined |
|
10 |
3.702 |
3.6457 |
0.6428 |
|
20 |
2.1164 |
1.9887 |
0.7238 |
|
30 |
1.557 |
1.3484 |
0.7785 |
|
40 |
1.28069 |
0.98106 |
0.8232 |
|
50 |
1.127 |
0.72442 |
0.86333 |
|
60 |
1.0427 |
0.52135 |
0.903 |
|
70 |
1.004588 |
0.34356 |
0.944 |
|
80 |
1.004588 |
0.17445 |
0.9893 |
|
90 |
1.0427 |
0 |
1.0427 |
|
100 |
1.127 |
-0.1957 |
1.109 |
|
110 |
1.28069 |
-0.43802 |
1.20345 |
|
120 |
1.127 |
-0.7785 |
1.3484 |
|
130 |
2.1164 |
-1.3604 |
1.6212 |
|
140 |
3.702 |
-2.8358 |
2.37959 |
|
150 |
Not defined |
Not defined |
Not defined |
Step by step
Solved in 7 steps with 43 images
