Medicare reimbursement regulations require no more than a 4% error rate in invoice coding from a service provider. You draw a random same of 75 invoices and, upon audit, find that there are 5 errors in the 75 invoices sampled. (a) If the true billing error rate for this service provider were no higher than 4%, what is the probability of having observed at least 5 errors in your sample? (b) Suppose you assert that this service provider does not meet the Medicare standard of no more than a 4% error rate. What is the false positive probability of your assertion? (c) If a provider’s true error coding rate were 4%, find the probability that a sample of 75 will result in between 1 to 5 coding errors, i.e., find where X is the number of coding errors.
Medicare reimbursement regulations require no more than a 4% error rate in invoice coding from a service provider. You draw a random same of 75 invoices and, upon audit, find that there are 5 errors in the 75 invoices sampled.
(a) If the true billing error rate for this service provider were no higher than 4%, what is the
(b) Suppose you assert that this service provider does not meet the Medicare standard of no more than a 4% error rate. What is the false positive probability of your assertion?
(c) If a provider’s true error coding rate were 4%, find the probability that a sample of 75 will result in between 1 to 5 coding errors, i.e., find where X is the number of coding errors.
Here, the distribution is Binomial with n=75 and p=0.04.
Hence, X~ Binomial(75,0.04).
The PMF is given by,
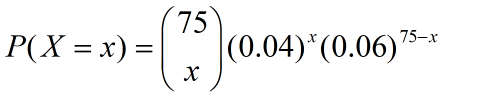
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 4 images




