maxima and minima. Use this information to sketch the curve. SOLUTION If f(x) = 3x - 24x³, then f'(x) = 12x - 72x² = 12x2(x - 6) f"(x) = 36x2 - 144x = 36x(x – 4). 6 To find the critical numbers we set f'(x) = 0 and obtain x = 0 and x = To use the Second Derivative Test we evaluate f" at these critical numbers: f"(0) = Video Example ) f"(6) = Since f'(6) = and f"(6) > 0, f(6) = is a local minimum. Since f"(0) = the Second Derivative Test gives no information about the critical number 0. But since f'(x) < 0 for x < 0 and also for 0
maxima and minima. Use this information to sketch the curve. SOLUTION If f(x) = 3x - 24x³, then f'(x) = 12x - 72x² = 12x2(x - 6) f"(x) = 36x2 - 144x = 36x(x – 4). 6 To find the critical numbers we set f'(x) = 0 and obtain x = 0 and x = To use the Second Derivative Test we evaluate f" at these critical numbers: f"(0) = Video Example ) f"(6) = Since f'(6) = and f"(6) > 0, f(6) = is a local minimum. Since f"(0) = the Second Derivative Test gives no information about the critical number 0. But since f'(x) < 0 for x < 0 and also for 0
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
100%
![EXAMPLE 6
Discuss the curve y = 3x* - 24x³ with respect to concavity, points of inflection, and local
maxima and minima. Use this information to sketch the curve.
SOLUTION If f(x) = 3x - 24x³, then
f'(x) = 12x3 - 72x² = 12x²(x - 6)
f"(x) = 36x2 - 144x = 36x(x – 4).
4
6
To find the critical numbers we set f'(x) = 0 and obtain x = 0 and x =
To use the Second
Derivative Test we evaluate f" at these critical numbers:
f"(0) =
Video Example )
f"(6) =
is a local minimum. Since f"(0) =
Since f'(6) =
Second Derivative Test gives no information about the critical number 0. But since f'(x) < 0 for x <0 and
also for 0 < x< 6, the First Derivative Test tells us that f does not have a local maximum or minimum at 0.
[In fact, the expression for f'(x) shows that f decreases to the left of 6 and increase to the right of 6.]
and f"(6) > 0, f(6) =
the
Since f"(x) = 0 when x = 0 or x =
we divide the real number line into intervals with these
numbers as endpoints and complete the following chart.
Interval
f"(x) = 36x(x - 4)
Concavity
(-00, 0)
upward
downward
upward
The point (0, 0) is an inflection point since the curve changes from concave upward to concave downward
(C
],
-768)
is an inflection point since the curve changes from concave downward to
there. Also,
concave upward there.
Using the local minimum, the intervals of concavity, and the inflection points, we sketch the curve in the figure.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F5abad2ef-7d64-4544-b6f7-dd3dfbff74f8%2Fc56b9b63-4570-4346-bc39-8e527176dcb3%2F0wrs0gs_processed.png&w=3840&q=75)
Transcribed Image Text:EXAMPLE 6
Discuss the curve y = 3x* - 24x³ with respect to concavity, points of inflection, and local
maxima and minima. Use this information to sketch the curve.
SOLUTION If f(x) = 3x - 24x³, then
f'(x) = 12x3 - 72x² = 12x²(x - 6)
f"(x) = 36x2 - 144x = 36x(x – 4).
4
6
To find the critical numbers we set f'(x) = 0 and obtain x = 0 and x =
To use the Second
Derivative Test we evaluate f" at these critical numbers:
f"(0) =
Video Example )
f"(6) =
is a local minimum. Since f"(0) =
Since f'(6) =
Second Derivative Test gives no information about the critical number 0. But since f'(x) < 0 for x <0 and
also for 0 < x< 6, the First Derivative Test tells us that f does not have a local maximum or minimum at 0.
[In fact, the expression for f'(x) shows that f decreases to the left of 6 and increase to the right of 6.]
and f"(6) > 0, f(6) =
the
Since f"(x) = 0 when x = 0 or x =
we divide the real number line into intervals with these
numbers as endpoints and complete the following chart.
Interval
f"(x) = 36x(x - 4)
Concavity
(-00, 0)
upward
downward
upward
The point (0, 0) is an inflection point since the curve changes from concave upward to concave downward
(C
],
-768)
is an inflection point since the curve changes from concave downward to
there. Also,
concave upward there.
Using the local minimum, the intervals of concavity, and the inflection points, we sketch the curve in the figure.
Expert Solution
Step 1
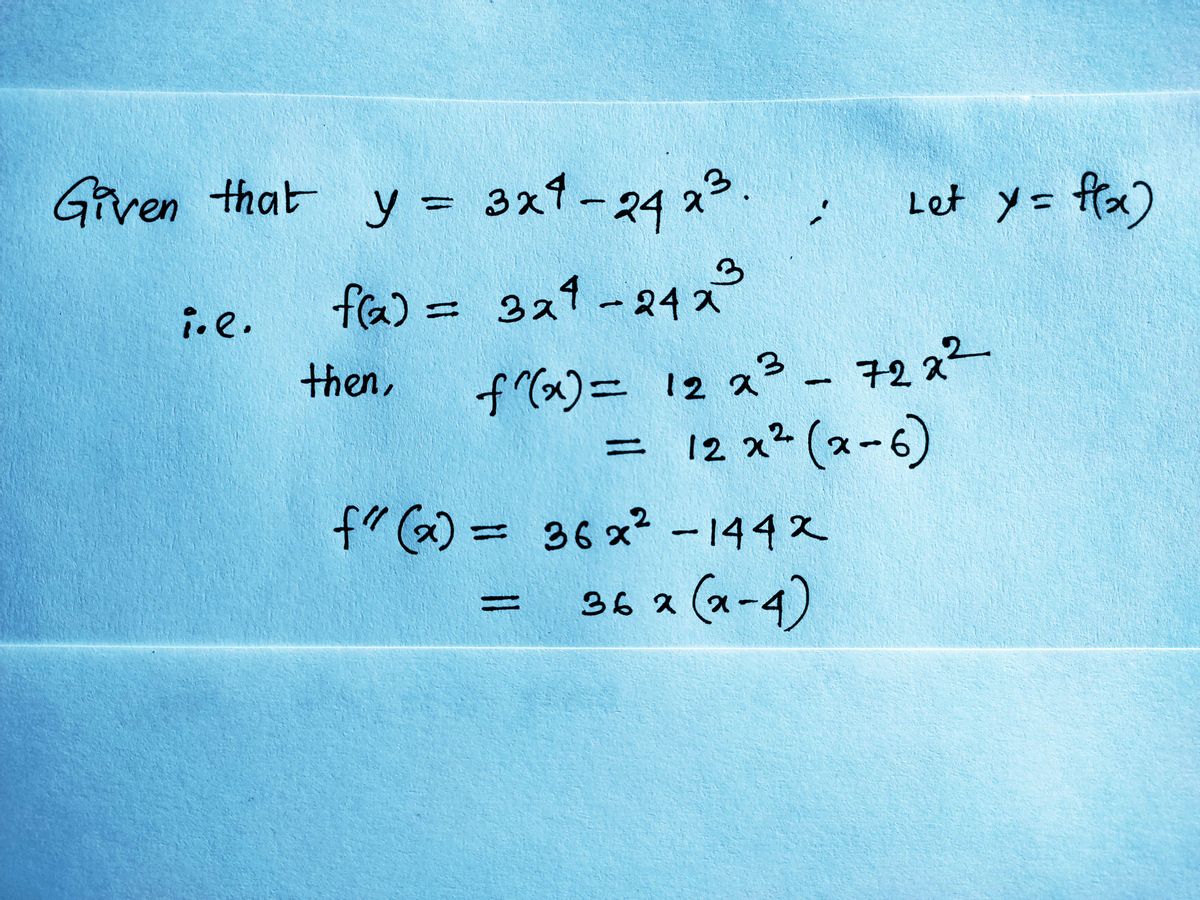
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning