M B C Mo EI (a) х tan B tan A Mo ГвA — Vв EI B IC/A = Vc 4 (b) (c) tan C
Determine the displacement of points B and C of the beam shown in Fig. a. EI is constant.

Given : A bending moment is applied at point C of the cantilever beam of length and is constant where is the young's modulus and is the moment of inertia.
To determine the deflection at point B and C we apply the application of area moment method which can be calculated as
and
The above method is valid when the point of zero slope is known that is the reference point and another point is the origin which is the point of non-zero slope.
The area moment diagram and point of deflection of the given cantilever beam is shown below
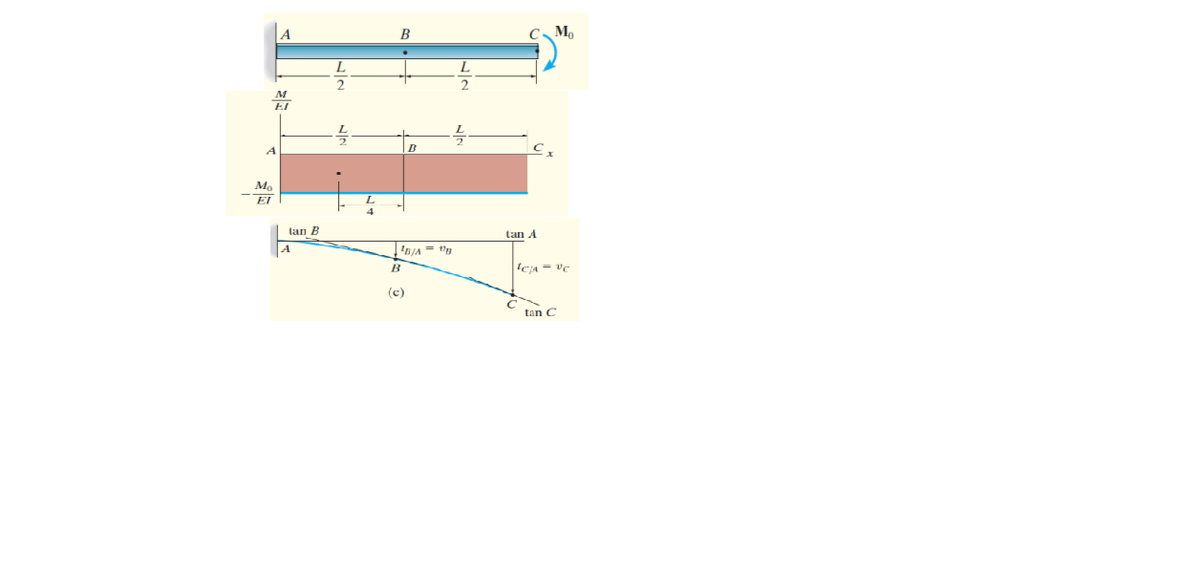
For displacement of point C-
The reference point that is point of zero slope is A and origin that is point of non zero slope is C
where and is the area of bending moment diagram while and is measured from the origin
Therefore
Step by step
Solved in 5 steps with 1 images









