Log-normal probability distribution A commonly used distribu- tion in probability and statistics is the log-normal distribution. (If the logarithm of a variable has a normal distribution, then the variable itself has a log-normal distribution.) The distribution function is 1 In'z/(20), for x 0, Xơ V2T f(x) where In x has zero mean and standard deviation o > 0. a. Graph f for o =5, 1, and 2. Based on your graphs, does lim f(x) appear to exist? b. Evaluate lim f(x). (Hint: Let x = e'.) c. Show that f has a single local maximum at x* = e¯". d. Evaluate f(x*) and express the result as a function of o. e. For what value of o > 0 in part (d) does f(x*) have a 2' minimum?
Log-normal probability distribution A commonly used distribu- tion in probability and statistics is the log-normal distribution. (If the logarithm of a variable has a normal distribution, then the variable itself has a log-normal distribution.) The distribution function is 1 In'z/(20), for x 0, Xơ V2T f(x) where In x has zero mean and standard deviation o > 0. a. Graph f for o =5, 1, and 2. Based on your graphs, does lim f(x) appear to exist? b. Evaluate lim f(x). (Hint: Let x = e'.) c. Show that f has a single local maximum at x* = e¯". d. Evaluate f(x*) and express the result as a function of o. e. For what value of o > 0 in part (d) does f(x*) have a 2' minimum?
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Log-normal probability distribution A commonly used distribu-
tion in probability and statistics is the log-normal distribution.
(If the logarithm of a variable has a normal distribution, then the
variable itself has a log-normal distribution.) The distribution
function is
1
In'z/(20), for x 0,
Xơ V2T
f(x)
where In x has zero mean and standard deviation o > 0.
a. Graph f for o =5, 1, and 2. Based on your graphs, does
lim f(x) appear to exist?
b. Evaluate lim f(x). (Hint: Let x = e'.)
c. Show that f has a single local maximum at x* = e¯".
d. Evaluate f(x*) and express the result as a function of o.
e. For what value of o > 0 in part (d) does f(x*) have a
2'
minimum?
Expert Solution
Step 1: Introduction
note :
Since you have posted question with multiple sub parts, we will provide the solution only to the first three sub parts of the question as per Q&A guidelines. Please repost the remaining question by specifying the sub parts need to be answered.

Step 2: Calculation (a)
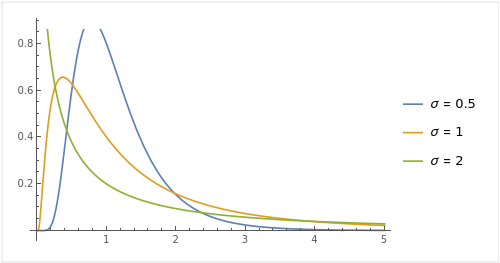

Step 3: Calculation (b)

Step by step
Solved in 5 steps with 5 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

