Locate the centroid of the plan area shown by integration. Smmmmmě mmmě mumě
Locate the centroid of the plan area shown by integration. Smmmmmě mmmě mumě
Chapter2: Loads On Structures
Section: Chapter Questions
Problem 1P
Related questions
Question
How to solve the question step by step

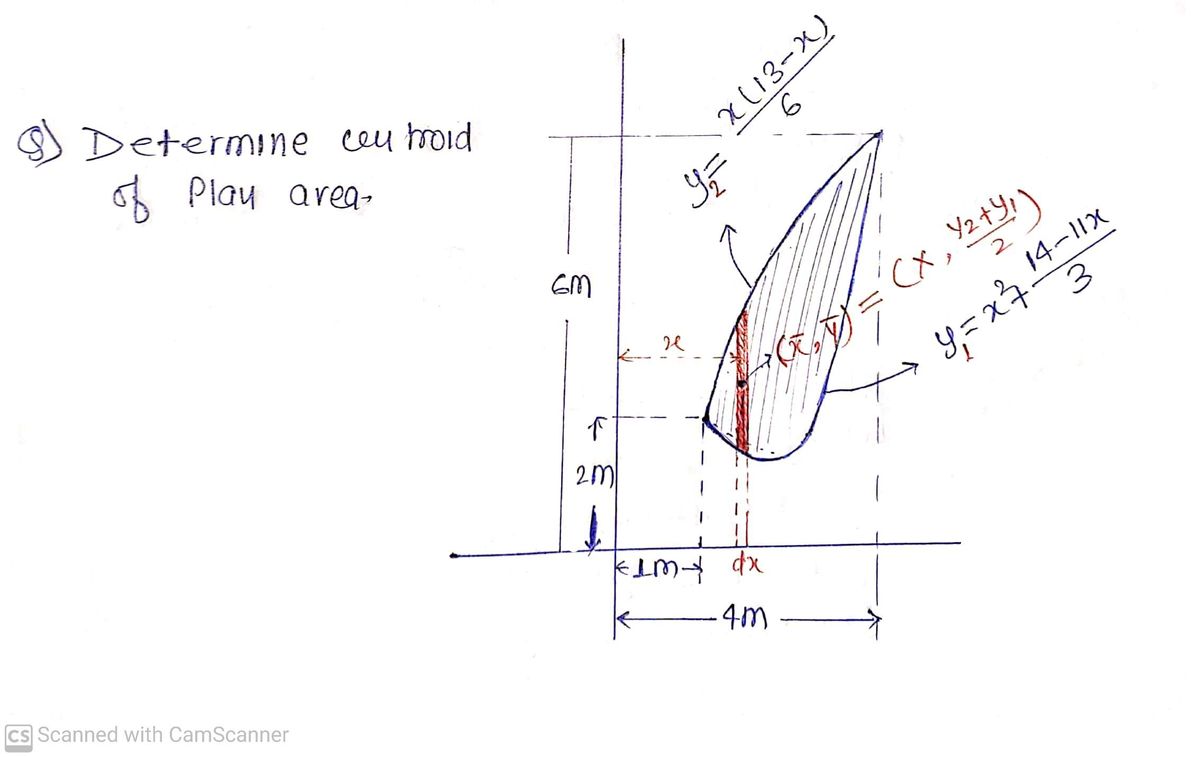
Transcribed Image Text:**Problem 5.4** - Locate the centroid of the plan area shown by integration.
This diagram features a two-dimensional, asymmetric triangular region described within a coordinate plane. It is utilized for finding the centroid through integration.
### Details:
- **Axes Configuration**:
- The x-axis is horizontal.
- The y-axis is vertical.
- **Boundary Descriptions**:
- The left boundary is defined by the line \( y = x(13 - x) \).
- The lower boundary is \( y = x^2 + \frac{14}{3} + 1.1x \).
- **Critical Points and Measurements**:
- The bottom-left corner of the area starts 1 m from the y-axis and 2 m above the x-axis.
- The area extends to the right, spanning a distance of 4 m.
- The top point of the boundary reaches 6 m along the y-axis.
- **Area**:
- Displays a complex boundary, requiring integration for centroid determination.
The grid in the background provides a reference for measurements with each square representing 1 square meter for easy calculation and visualization. The shaded region and the mathematical expressions signify the area of interest for calculating the centroid, employing calculus techniques.
Expert Solution
Step 1
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you


Structural Analysis (10th Edition)
Civil Engineering
ISBN:
9780134610672
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning


Structural Analysis (10th Edition)
Civil Engineering
ISBN:
9780134610672
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning

Fundamentals of Structural Analysis
Civil Engineering
ISBN:
9780073398006
Author:
Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel Lanning
Publisher:
McGraw-Hill Education


Traffic and Highway Engineering
Civil Engineering
ISBN:
9781305156241
Author:
Garber, Nicholas J.
Publisher:
Cengage Learning