Listed below are the annual tuition amounts of the 10 most expensive colleges in a country for a recent year. What does this "Top 10" list tell us about the population of all of that country's college tuitions? $52,768 $52,184 $52,768 $53,626 $50,815 O $50,918 $52,471 $53,616 $52,874 $53,847 The mean of the data set is $ (Round to two decimal places as needed.) The midrange of the data set is $ (Round to two decimal places as needed.) The median of the data set is $. (Round to two decimal places as needed.) What is (are) the mode(s) of the data set? Select the correct choice below and, if necessary, fill in the answer box within your choice. O A. The mode(s) of the data set is (are) $. (Use comma to separate answers as needed. Round to two decimal places as needed.) O B. There is no mode. What does this "Top 10" list tell us about the population of all the country's college tuitions? O A. All colleges have tuitions around the median, O B. All colleges have tuitions around the mode. O C. All colleges have tuitions around the mean.
Inverse Normal Distribution
The method used for finding the corresponding z-critical value in a normal distribution using the known probability is said to be an inverse normal distribution. The inverse normal distribution is a continuous probability distribution with a family of two parameters.
Mean, Median, Mode
It is a descriptive summary of a data set. It can be defined by using some of the measures. The central tendencies do not provide information regarding individual data from the dataset. However, they give a summary of the data set. The central tendency or measure of central tendency is a central or typical value for a probability distribution.
Z-Scores
A z-score is a unit of measurement used in statistics to describe the position of a raw score in terms of its distance from the mean, measured with reference to standard deviation from the mean. Z-scores are useful in statistics because they allow comparison between two scores that belong to different normal distributions.

Mean: The mean is the sum of observations divided by the number of observations. that is,
Mean =
Notations:
The sample mean = and
Population mean = μ
Range = Maximum - Minimum
Median: The median is the value of the middlemost observation in the data set when the observation is arranged in increasing (or decreasing) order of their values.
Formula for median:
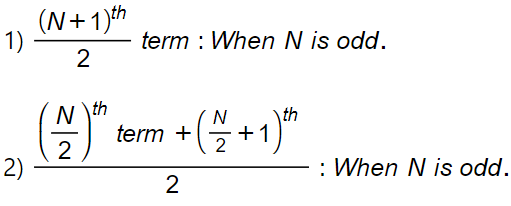
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 2 images









