Listed below are paired data consisting of amounts spent on advertising (in millions of dollars) and the profits (in millions of dollars). Determine if there is a significant positive linear correlation between advertising cost and profit . Use a significance level of 0.01 and round all values to 4 decimal places.
Correlation
Correlation defines a relationship between two independent variables. It tells the degree to which variables move in relation to each other. When two sets of data are related to each other, there is a correlation between them.
Linear Correlation
A correlation is used to determine the relationships between numerical and categorical variables. In other words, it is an indicator of how things are connected to one another. The correlation analysis is the study of how variables are related.
Regression Analysis
Regression analysis is a statistical method in which it estimates the relationship between a dependent variable and one or more independent variable. In simple terms dependent variable is called as outcome variable and independent variable is called as predictors. Regression analysis is one of the methods to find the trends in data. The independent variable used in Regression analysis is named Predictor variable. It offers data of an associated dependent variable regarding a particular outcome.


Correlation:
The correlation value is obtained using EXCEL. The software procedure is given below:
- Enter the data.
- Select Data > Data Analysis >Correlation> OK.
- Enter Input Range as A1:B11.
- Mark Labels in First Row.
- Click OK.
The output using EXCEL is as follows:
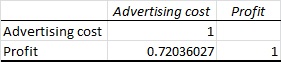
From the output, the correlation coefficient is 0.7204.
Thus, the linear correlation coefficient is 0.7204.
Step by step
Solved in 2 steps with 1 images









