Let X and Y be discrete random variables that take the values 1,2, ... N with equal probability, where N is a positive integer. X and Y are independent, so in particular P(X ≤a and Y ≤ b) = P(X ≤ a)P(Y≤ b). Let Z max (X, Y). Note that Z is also a random variable that takes = values from 1 to N. a. Write down the probability distribution function for X (which is also the probability distribution function for Y). b. Find the expected value of X c. Find P(Z < 20) (Hint: Your answer will involve the parameter N. There are two cases: what are they? Note also that max (X, Y) ≤ 20 if and only if both X ≤ 20 and Y ≤ 20). d. Find the cdf of Z. (Hint: Write down the definition of F₂(x).) e. Using the cdf from part d., find the probability distribution function for Z. (NOTE I am being very specific here. You MUST use the cdf of to do this problem. If you do it a different way, you receive no credit.) f. Find EIZ). (Hint: you will need the formulas for E-₁n and -₁²) n n=1 E[Z] g. Find limy co 100 E[X]' and comment on your answer. Can you think of a practical situation in which this information might be useful?
Let X and Y be discrete random variables that take the values 1,2, ... N with equal probability, where N is a positive integer. X and Y are independent, so in particular P(X ≤a and Y ≤ b) = P(X ≤ a)P(Y≤ b). Let Z max (X, Y). Note that Z is also a random variable that takes = values from 1 to N. a. Write down the probability distribution function for X (which is also the probability distribution function for Y). b. Find the expected value of X c. Find P(Z < 20) (Hint: Your answer will involve the parameter N. There are two cases: what are they? Note also that max (X, Y) ≤ 20 if and only if both X ≤ 20 and Y ≤ 20). d. Find the cdf of Z. (Hint: Write down the definition of F₂(x).) e. Using the cdf from part d., find the probability distribution function for Z. (NOTE I am being very specific here. You MUST use the cdf of to do this problem. If you do it a different way, you receive no credit.) f. Find EIZ). (Hint: you will need the formulas for E-₁n and -₁²) n n=1 E[Z] g. Find limy co 100 E[X]' and comment on your answer. Can you think of a practical situation in which this information might be useful?
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
Please answer d-g
![1. Let X and Y be discrete random variables that take the values 1,2, ... N with equal probability,
where N is a positive integer. X and Y are independent, so in particular P(X ≤ a and Y ≤ b)
= P(X ≤ a)P(Y ≤ b). Let Z = max(X, Y). Note that Z is also a random variable that takes
values from 1 to N.
a. Write down the probability distribution function for X (which is also the probability
distribution function for Y).
b. Find the expected value of X
c. Find P(Z < 20)
(Hint: Your answer will involve the parameter N. There are two cases: what are they?
Note also that max (X, Y) ≤ 20 if and only if both X ≤ 20 and Y ≤ 20).
d. Find the cdf of Z. (Hint: Write down the definition of F₂(x).)
e. Using the cdf from part d., find the probability distribution function for Z. (NOTE I am
being very specific here. You MUST use the cdf of to do this problem. If you do it a
different way, you receive no credit.)
2
f. Find E[Z]. (Hint: you will need the formulas for EN-1n and Σ=1
N
g. Find limy→∞
E[2], and comment on your answer. Can you think of a practical situation
E[X]'
in which this information might be useful?
n](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fa86feb48-aed4-4133-a748-653f8a12a813%2F442755ff-7b9c-4850-890d-4fa18e5d52e2%2Fyt3mtno_processed.jpeg&w=3840&q=75)
Transcribed Image Text:1. Let X and Y be discrete random variables that take the values 1,2, ... N with equal probability,
where N is a positive integer. X and Y are independent, so in particular P(X ≤ a and Y ≤ b)
= P(X ≤ a)P(Y ≤ b). Let Z = max(X, Y). Note that Z is also a random variable that takes
values from 1 to N.
a. Write down the probability distribution function for X (which is also the probability
distribution function for Y).
b. Find the expected value of X
c. Find P(Z < 20)
(Hint: Your answer will involve the parameter N. There are two cases: what are they?
Note also that max (X, Y) ≤ 20 if and only if both X ≤ 20 and Y ≤ 20).
d. Find the cdf of Z. (Hint: Write down the definition of F₂(x).)
e. Using the cdf from part d., find the probability distribution function for Z. (NOTE I am
being very specific here. You MUST use the cdf of to do this problem. If you do it a
different way, you receive no credit.)
2
f. Find E[Z]. (Hint: you will need the formulas for EN-1n and Σ=1
N
g. Find limy→∞
E[2], and comment on your answer. Can you think of a practical situation
E[X]'
in which this information might be useful?
n
Expert Solution
Step 1: pmf and cdf obtained
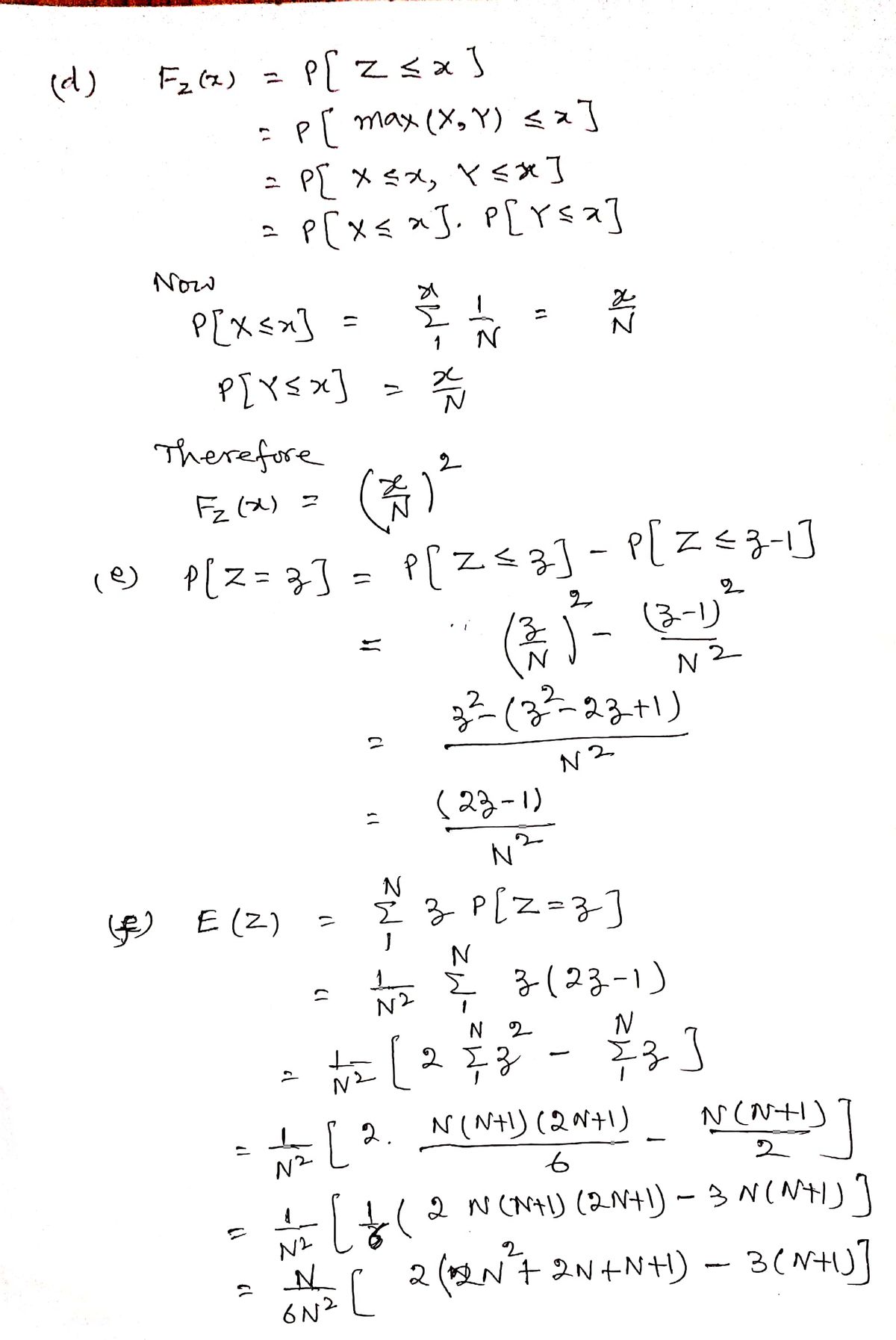
Step by step
Solved in 3 steps with 7 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
