Let V R. For u, v E V and a € R define vector addition by uv : u+v+2 and scalar multiplication by au : au +2a - 2. It can be shown that (V,B, ) is a vector space over Find the following: the scalar field R. the sum: -9-9= the scalar multiple: -30-9- the zero vector: Oy = the additive inverse of a: Bx =
Let V R. For u, v E V and a € R define vector addition by uv : u+v+2 and scalar multiplication by au : au +2a - 2. It can be shown that (V,B, ) is a vector space over Find the following: the scalar field R. the sum: -9-9= the scalar multiple: -30-9- the zero vector: Oy = the additive inverse of a: Bx =
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Let V = R. For u, v € V and a ER define vector addition by uvu+v + 2 and scalar multiplication by au= au +2a - 2. It can be shown that (V,B, ) is a vector space over
the scalar field R. Find the following:
the sum:
-9-9=
the scalar multiple:
-3-9=
the zero vector:
Ov
the additive inverse of a
Bx
Expert Solution
Step 1: Given information
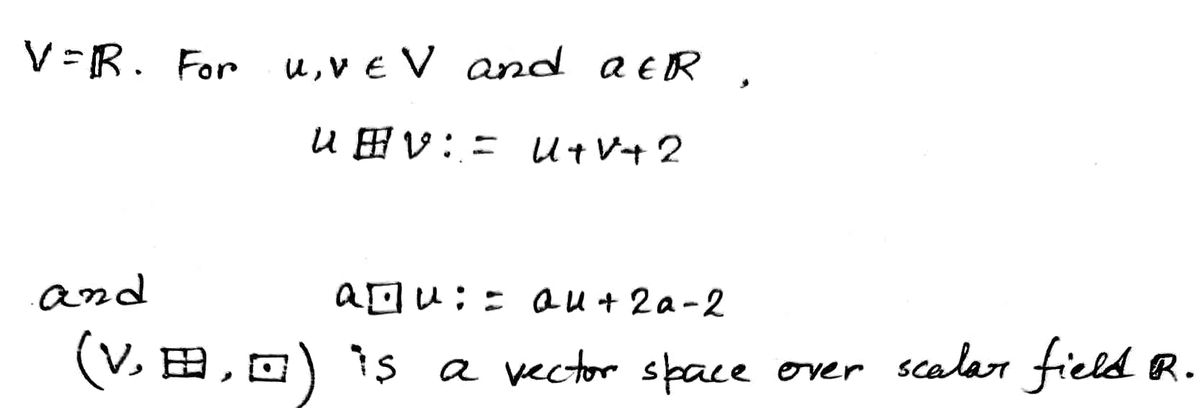
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

