Let T denote the lifetime of an individual having the cumulative distribution function - Exp(-+-+²). F(t) = P(T ≤ t) = 1 - exp Denote by Tx := T − x the remaining lifetime of an individual aged x > 0. The curtate lifetime Kx = [Tx] defines the integer part of T, as such that P(Kx = k) = P(k ≤ Tx < k + 1). (a) Specify the survival distribution Sx(t) := P(Tx > t) of individual aged x. (b) Determine the mortality rate of the individual by working out the limit below µx(t) := lim - P(t ≤ Tx < t + h|Tx ≥ t) ho h (c) Find the probability mass function P(Kx = k) of curtate lifetime Kx. (d) Show that the expected curtate lifetime E[K,] is given by the following formula ∞ E[K] = P(Tx ≥k). k=1
Let T denote the lifetime of an individual having the cumulative distribution function - Exp(-+-+²). F(t) = P(T ≤ t) = 1 - exp Denote by Tx := T − x the remaining lifetime of an individual aged x > 0. The curtate lifetime Kx = [Tx] defines the integer part of T, as such that P(Kx = k) = P(k ≤ Tx < k + 1). (a) Specify the survival distribution Sx(t) := P(Tx > t) of individual aged x. (b) Determine the mortality rate of the individual by working out the limit below µx(t) := lim - P(t ≤ Tx < t + h|Tx ≥ t) ho h (c) Find the probability mass function P(Kx = k) of curtate lifetime Kx. (d) Show that the expected curtate lifetime E[K,] is given by the following formula ∞ E[K] = P(Tx ≥k). k=1
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
I need this question completed in 5 minutes with handwritten working
![3. Let T denote the lifetime of an individual having the cumulative distribution function
- exp(-1/²)
F(t) = P(T ≤t) = 1 - exp
Denote by Tx := T − x the remaining lifetime of an individual aged x > 0.
The curtate lifetime Kx = [Tx] defines the integer part of Tx as such that
P(Kx = k) = P(k ≤ Tx < k + 1).
(a) Specify the survival distribution S x(t) := P(Tx > t) of individual aged x.
(b) Determine the mortality rate of the individual by working out the limit below
ux(t): lim -P(t ≤ Tx < t + h|Tx ≥ t)
ho h
(c) Find the probability mass function P(K, = k) of curtate lifetime K.
(d) Show that the expected curtate lifetime E[K] is given by the following formula
∞
E[Kx] = ΣP(Tx ≥ k).
k=1](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fba18de34-fc06-47a6-b1ea-c54726b84874%2F7d879d04-2718-4b2d-a139-4cb5e6249874%2Fcs27su4_processed.png&w=3840&q=75)
Transcribed Image Text:3. Let T denote the lifetime of an individual having the cumulative distribution function
- exp(-1/²)
F(t) = P(T ≤t) = 1 - exp
Denote by Tx := T − x the remaining lifetime of an individual aged x > 0.
The curtate lifetime Kx = [Tx] defines the integer part of Tx as such that
P(Kx = k) = P(k ≤ Tx < k + 1).
(a) Specify the survival distribution S x(t) := P(Tx > t) of individual aged x.
(b) Determine the mortality rate of the individual by working out the limit below
ux(t): lim -P(t ≤ Tx < t + h|Tx ≥ t)
ho h
(c) Find the probability mass function P(K, = k) of curtate lifetime K.
(d) Show that the expected curtate lifetime E[K] is given by the following formula
∞
E[Kx] = ΣP(Tx ≥ k).
k=1
Expert Solution
Step 1: Survival distribution obtained
As per guidelines of the Bartleby, solution of only first 3 parts are given.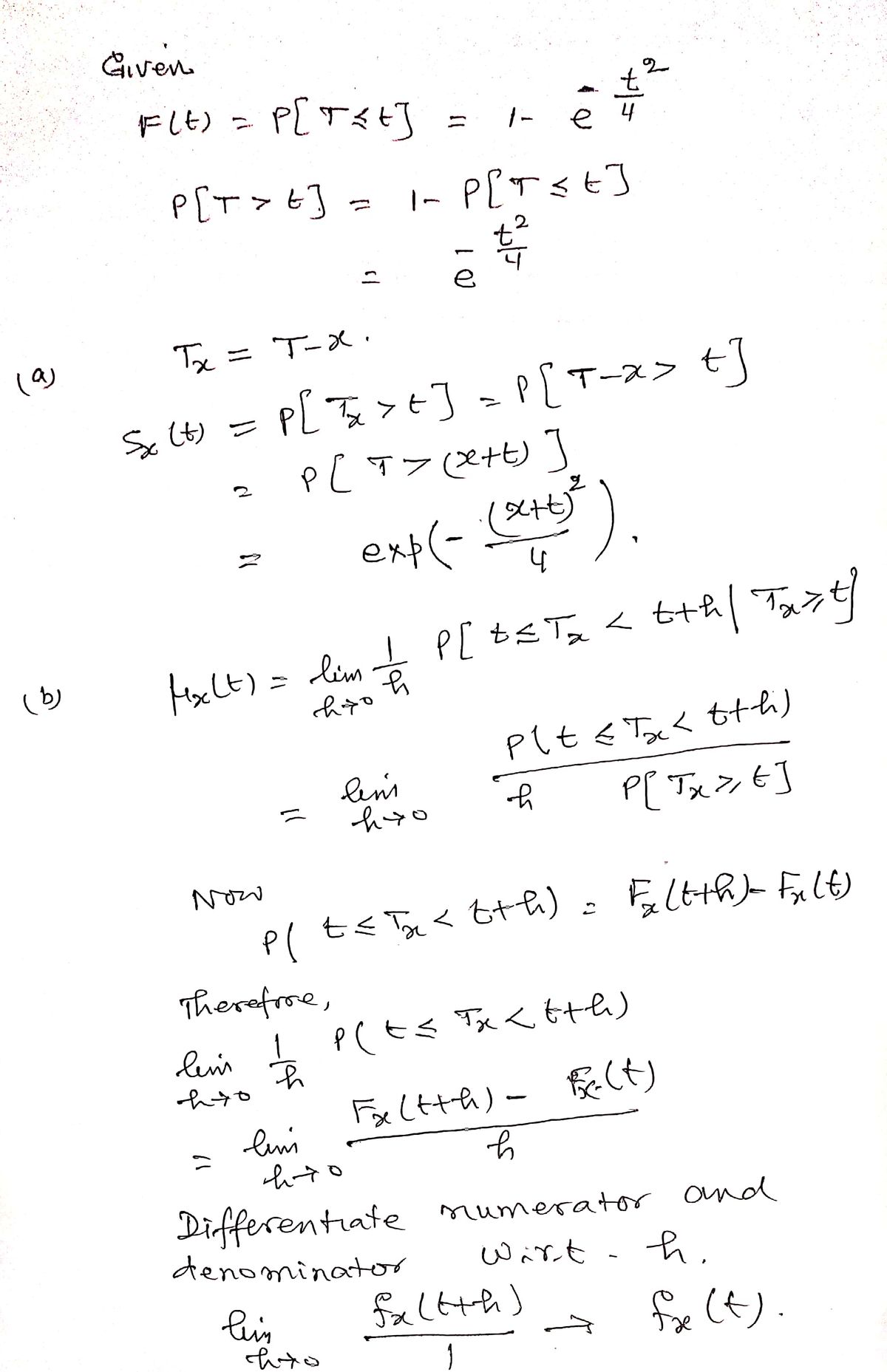
Step by step
Solved in 3 steps with 5 images

Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman