Let L be a language over the alphabet Σ = {a, b}. Prove that
Database System Concepts
7th Edition
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Chapter1: Introduction
Section: Chapter Questions
Problem 1PE
Related questions
Question
Only B Please!

Transcribed Image Text:A The pumping length of the following deterministic finite automata is 4 because there are four states.
0
0,1
Q3
*
0
0
1
1
Q2
Answer the following:
1. State a string of length 4 or greater that is accepted by the deterministic finite automaton
2. Decompose the string into the x, y, and z substrings so that the conclusions of the pumping lemma holds,
and,
3. Highlight a loop in the state diagram that corresponds to the substring y.
B Let L be a language over the alphabet Σ = {a, b}.
Prove that
L = {akb2k for any integer k ≥ 0}
is not regular.
Proof: Assume that L is regular, so that the pumping lemma applies. Therefore L has a pumping length p.
Let s =
Since s belongs to
This string is a member of L because
L and has length longer than p, there exist strings x, y, and z such that s = xyz, where
* xz is a member of L,
*xy'z is a member of L for all positive integers i,
* y >0, and
|xy| ≤p.
Now consider the following argument: (You finish the rest of the proof.)
Expert Solution
Step 1: Given
Consider the given statement :
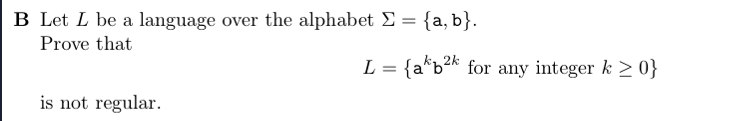
Step by step
Solved in 3 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Recommended textbooks for you

Database System Concepts
Computer Science
ISBN:
9780078022159
Author:
Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:
McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:
9780134444321
Author:
Tony Gaddis
Publisher:
PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:
9780132737968
Author:
Thomas L. Floyd
Publisher:
PEARSON

Database System Concepts
Computer Science
ISBN:
9780078022159
Author:
Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:
McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:
9780134444321
Author:
Tony Gaddis
Publisher:
PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:
9780132737968
Author:
Thomas L. Floyd
Publisher:
PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:
9780133976892
Author:
Paul J. Deitel, Harvey Deitel
Publisher:
PEARSON

Database Systems: Design, Implementation, & Manag…
Computer Science
ISBN:
9781337627900
Author:
Carlos Coronel, Steven Morris
Publisher:
Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education