Let h(t) = 4t – Vt2 + 1. Determine any critical points of h.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:```markdown
Let \( h(t) = 4t - \sqrt{t^2 + 1} \). Determine any critical points of \( h \).
```
To find the critical points of the function \( h(t) = 4t - \sqrt{t^2 + 1} \), we need to calculate its derivative and find where it is equal to zero or undefined.
1. **Calculate the Derivative:**
- Differentiate \( h(t) = 4t - (t^2 + 1)^{1/2} \).
- Use the chain rule for the second term.
2. **Solve for Critical Points:**
- Set the derivative equal to zero and solve for \( t \).
- Identify any points where the derivative does not exist.
3. **Analyze the Critical Points:**
- Use the first or second derivative test to classify the critical points as local maxima, minima, or points of inflection.
Include any diagrams or graphs that help illustrate the changes in the function's slope around the critical points for visual assistance.
Expert Solution
Step 1
We have to find critical point of h:

Step 2
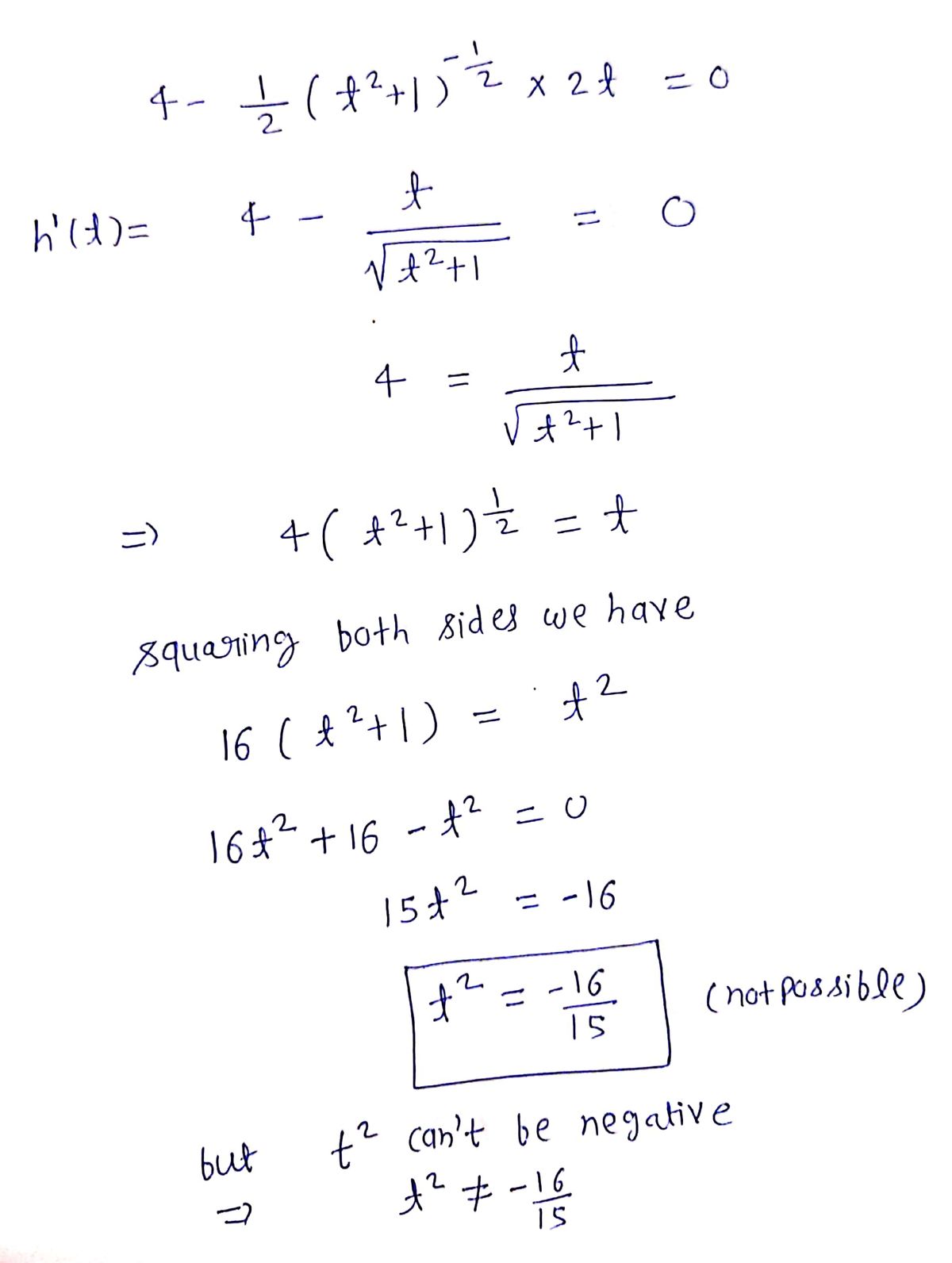
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

