Let f: Nx N → Z defined by f(n, m) = n − m² 1. Find f({(0, 0), (1,0), (0, 1), (1, 1)}) 2. find f-¹({0}) 3. Determine whether f is one-to-one (or injective). Note: f¹(B) denotes the set of pre-images of B by f for any B subset of the codomain of f.
Let f: Nx N → Z defined by f(n, m) = n − m² 1. Find f({(0, 0), (1,0), (0, 1), (1, 1)}) 2. find f-¹({0}) 3. Determine whether f is one-to-one (or injective). Note: f¹(B) denotes the set of pre-images of B by f for any B subset of the codomain of f.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:Let f: Nx N → Z defined by f(n, m) = n − m²
1. Find f({(0, 0), (1,0), (0, 1), (1, 1)})
2. find f-¹({0})
3. Determine whether f is one-to-one (or injective).
Note: f¹(B) denotes the set of pre-images of B by f for
any B subset of the codomain of f.
Expert Solution
Step 1
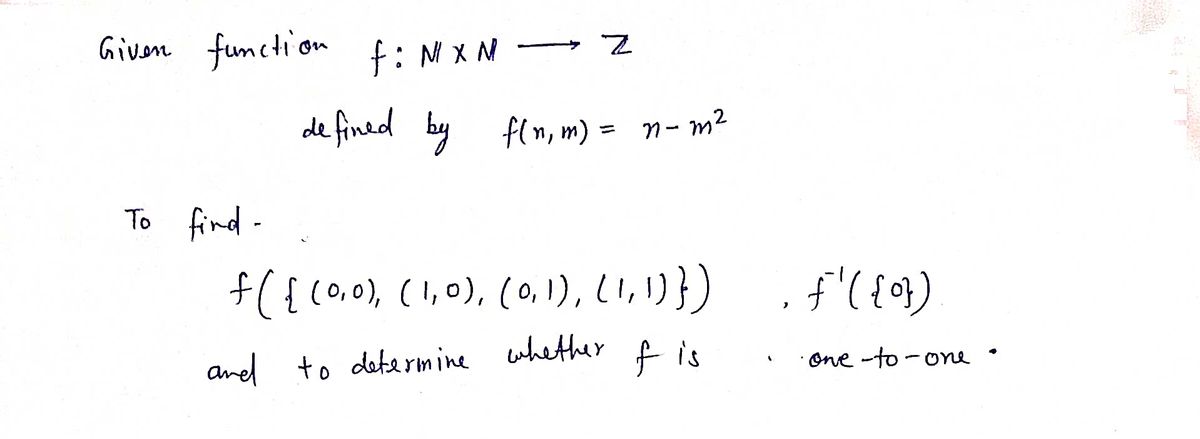
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

