Let e,= The image of and e₂= , and y₂² 7 and let T: R² R2 be a linear transformation that maps e, into y, and maps e into y₂. Find the images of 5 and
Let e,= The image of and e₂= , and y₂² 7 and let T: R² R2 be a linear transformation that maps e, into y, and maps e into y₂. Find the images of 5 and
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
1.8 #6

Transcribed Image Text:**Title: Linear Transformation and Vector Image Mapping**
**Description:**
This problem involves understanding linear transformations in the context of mapping vectors.
**Given:**
- Vectors:
- \( e_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \)
- \( e_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \)
- \( y_1 = \begin{bmatrix} 3 \\ 6 \end{bmatrix} \)
- \( y_2 = \begin{bmatrix} -1 \\ 7 \end{bmatrix} \)
- Transformation:
- Let \( T: \mathbb{R}^2 \to \mathbb{R}^2 \) be a linear transformation that maps \( e_1 \) into \( y_1 \) and \( e_2 \) into \( y_2 \).
**Objective:**
- Find the images of:
- \( \begin{bmatrix} 5 \\ -3 \end{bmatrix} \)
- \( \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \)
**Instructions:**
1. Use the properties of linear transformations to express any vector in terms of its basis vectors.
2. Apply the transformation \( T \) to the given vectors, utilizing the mapping of \( e_1 \) to \( y_1 \) and \( e_2 \) to \( y_2 \).
**Solution Approach:**
1. **Mapping Setup:**
- Determine how the transformation \( T \) affects a general vector \( \begin{bmatrix} x \\ y \end{bmatrix} = x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix} \).
2. **Transformation Application:**
- \( T\left(\begin{bmatrix} x \\ y \end{bmatrix}\right) = x T\left(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\right) + y T\left(\begin{bmatrix} 0 \\ 1 \end{bmatrix}\right) \)
- Substitute the known transformations:
- \( T\
Expert Solution
Step 1
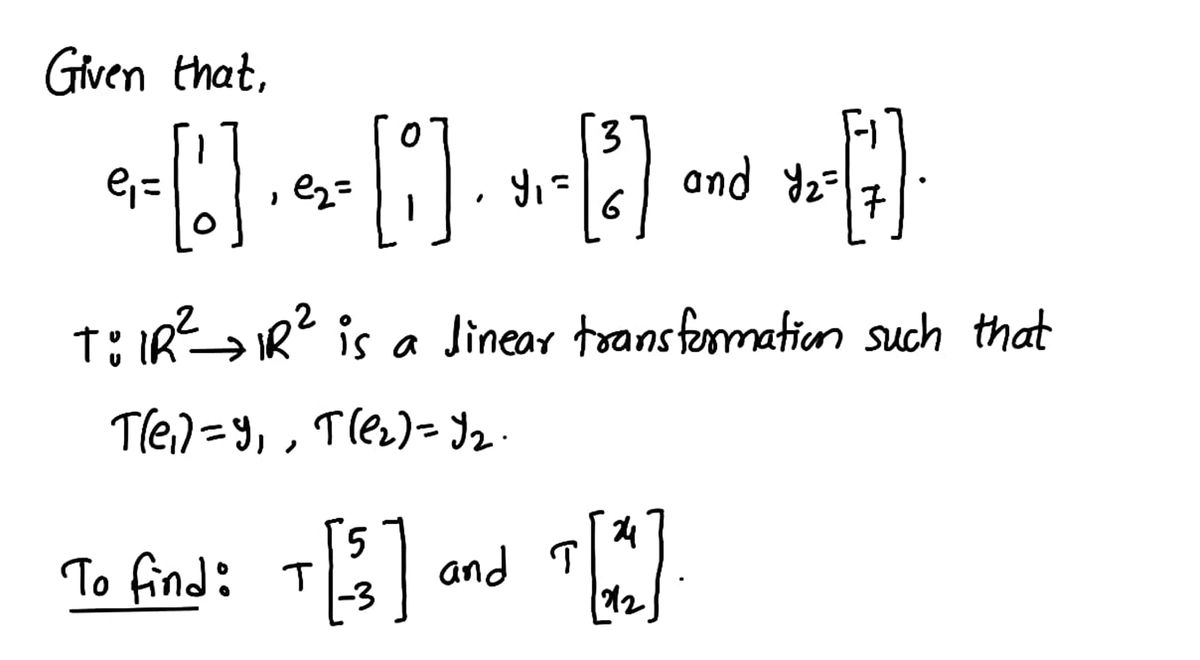
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

