Let C'(x) be the cost (in dollars) of producing units of a product per day. Suppose C(99) = 90 and C' (99)=-6. Estimate the cost of producing 100 items per day.
Let C'(x) be the cost (in dollars) of producing units of a product per day. Suppose C(99) = 90 and C' (99)=-6. Estimate the cost of producing 100 items per day.
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Problem Statement:**
Let \( C(x) \) be the cost (in dollars) of producing \( x \) units of a product per day. Suppose \( C(99) = 90 \) and \( C'(99) = -6 \). Estimate the cost of producing 100 items per day.
**Solution:**
To estimate the cost of producing 100 items, we can use the information given and apply the concept of linear approximations or differentials. The derivative \( C'(99) \) gives us the rate at which the cost is changing at the production level of 99 units.
Given:
- \( C(99) = 90 \)
- \( C'(99) = -6 \)
We can approximate \( C(100) \) using the formula for linear approximation:
\[ C(100) \approx C(99) + C'(99) \times (100 - 99) \]
Substituting the known values:
\[ C(100) \approx 90 + (-6) \times 1 \]
\[ C(100) \approx 90 - 6 \]
\[ C(100) \approx 84 \]
Therefore, the estimated cost of producing 100 items per day is approximately $84.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2ee05961-48f0-4164-984e-730a8b15f9ee%2F9a11108c-f49f-4e62-b3a0-8b690b1f08f8%2F4vrnbqs_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Let \( C(x) \) be the cost (in dollars) of producing \( x \) units of a product per day. Suppose \( C(99) = 90 \) and \( C'(99) = -6 \). Estimate the cost of producing 100 items per day.
**Solution:**
To estimate the cost of producing 100 items, we can use the information given and apply the concept of linear approximations or differentials. The derivative \( C'(99) \) gives us the rate at which the cost is changing at the production level of 99 units.
Given:
- \( C(99) = 90 \)
- \( C'(99) = -6 \)
We can approximate \( C(100) \) using the formula for linear approximation:
\[ C(100) \approx C(99) + C'(99) \times (100 - 99) \]
Substituting the known values:
\[ C(100) \approx 90 + (-6) \times 1 \]
\[ C(100) \approx 90 - 6 \]
\[ C(100) \approx 84 \]
Therefore, the estimated cost of producing 100 items per day is approximately $84.
Expert Solution
Step 1
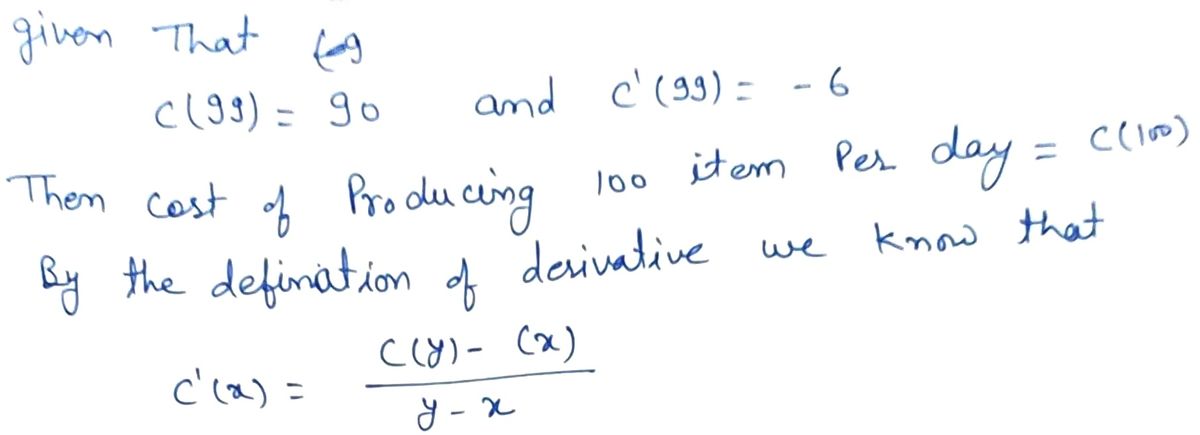
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning