Let B = b₂ = 3c₁ - 2c₂. be bases for a vector space V, and suppose b₁ = {C₁,C₂} {b₁,b₂} and C= a. Find the change-of-coordinates matrix from B to C. b. Find [x]c for x = − 2b₁ +5b₂. Use part (a). -7c₁ +8c2 and ==
Let B = b₂ = 3c₁ - 2c₂. be bases for a vector space V, and suppose b₁ = {C₁,C₂} {b₁,b₂} and C= a. Find the change-of-coordinates matrix from B to C. b. Find [x]c for x = − 2b₁ +5b₂. Use part (a). -7c₁ +8c2 and ==
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Hello there, can you help me solve problem? Thank you!
![{b₁
$1,0₂2}
b₂ = 3c₁-2c₂.
Let B =
=
and C= {C₁,C₂} be bases for a vector space V, and suppose b₁
a. Find the change-of-coordinates matrix from B to C.
b. Find [x]c for x = − 2b₁ +5b₂. Use part (a).
- 7c₁ + 8c₂ and](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe00cebfb-aec4-474d-8979-79a2d105b819%2F52352353-25d2-4ff6-9feb-75723ddb6b3f%2Fhguxbkq_processed.png&w=3840&q=75)
Transcribed Image Text:{b₁
$1,0₂2}
b₂ = 3c₁-2c₂.
Let B =
=
and C= {C₁,C₂} be bases for a vector space V, and suppose b₁
a. Find the change-of-coordinates matrix from B to C.
b. Find [x]c for x = − 2b₁ +5b₂. Use part (a).
- 7c₁ + 8c₂ and
![Let A = {a₁,a2,a3} and B = {b₁,b2,b3} be bases for a vector space V, and suppose a₁ = 2b₁ b₂,
2= -b₁ +4b₂ + b3, a3 =b₂-3b3.
a2
a. Find the
change-of-coordinates matrix from A to B.
b. Find [x] for x = 3a₁ + a₂ + a3.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe00cebfb-aec4-474d-8979-79a2d105b819%2F52352353-25d2-4ff6-9feb-75723ddb6b3f%2Fywzxqj_processed.png&w=3840&q=75)
Transcribed Image Text:Let A = {a₁,a2,a3} and B = {b₁,b2,b3} be bases for a vector space V, and suppose a₁ = 2b₁ b₂,
2= -b₁ +4b₂ + b3, a3 =b₂-3b3.
a2
a. Find the
change-of-coordinates matrix from A to B.
b. Find [x] for x = 3a₁ + a₂ + a3.
Expert Solution
Step 1: Question 1
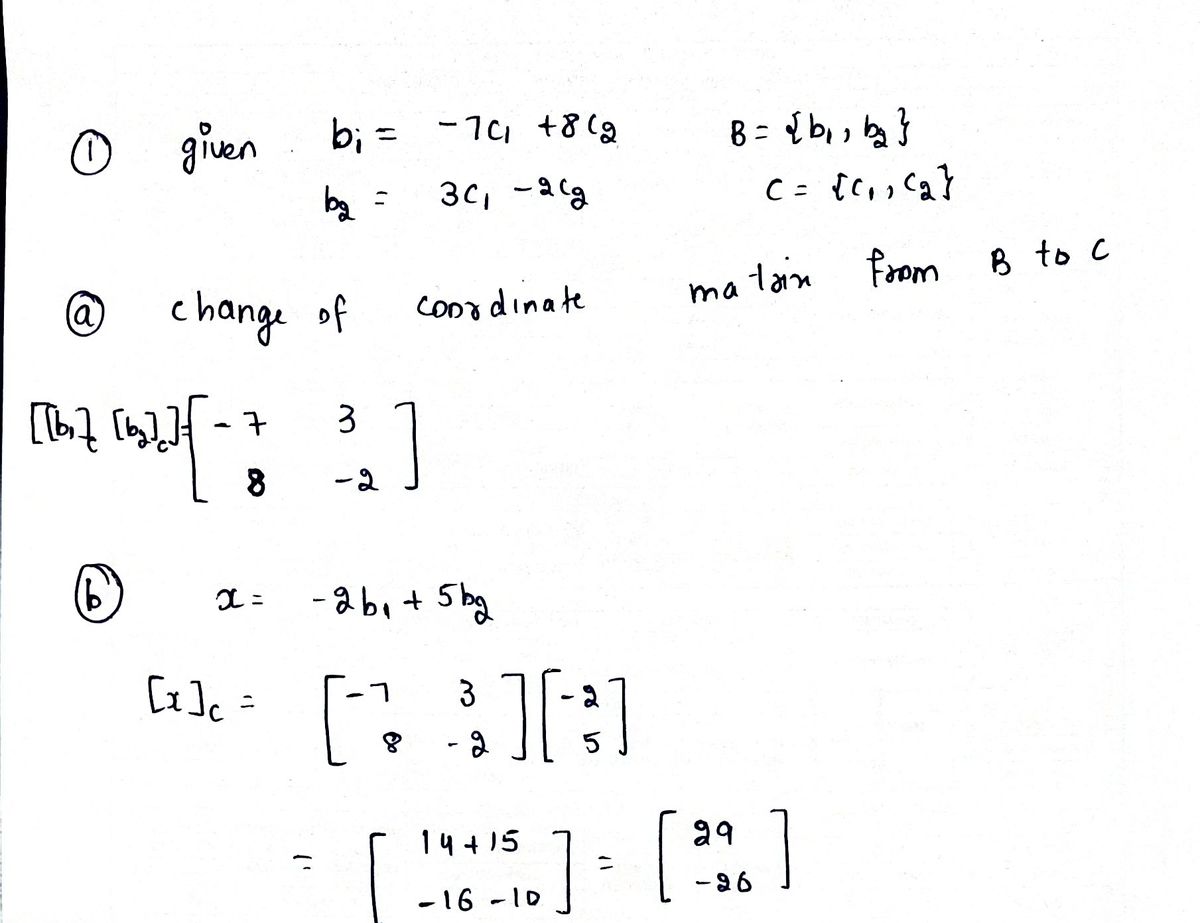
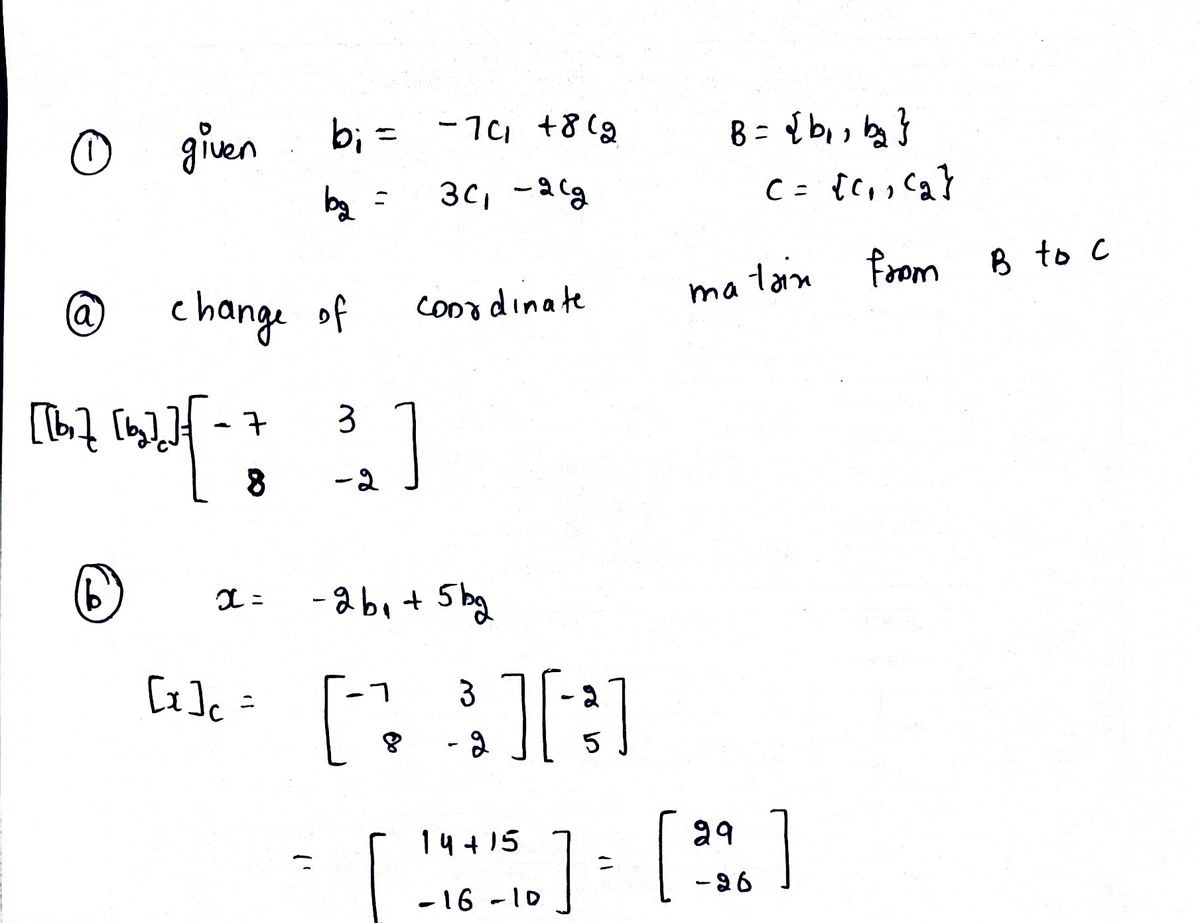
Step by step
Solved in 4 steps with 5 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

