Let An denote the number of lattice paths from (0,0) to (n, n) that do not pass above the diagonal y = x. Find A₁, A2, A3, and A4.
Let An denote the number of lattice paths from (0,0) to (n, n) that do not pass above the diagonal y = x. Find A₁, A2, A3, and A4.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Help!! Help!!
![**Problem Set on Combinatorics**
a. Let \( A_n \) denote the number of lattice paths from \((0, 0)\) to \((n, n)\) that do not pass above the diagonal \( y = x \). Find \( A_1, A_2, A_3, \) and \( A_4 \).
b. Let \( B_n \) denote the number of expressions containing \( n \) pairs of parentheses which are correctly matched. For example, \( B_2 = 2 \), since \(()() \) and \( (()) \) are the only two sets of correctly matched parentheses. Compute \( B_1, B_2, B_3, \) and \( B_4 \).
c. A **standard tableau** of shape \( 2 \times n \) is a \( 2 \times n \)-grid filled with the numbers 1, 2, \ldots, 2n, using each number once, so that every row increases left to right and every column increases top to bottom. For example, there are 2 standard tableaux of shape \( 2 \times 2 \):
\[
\begin{array}{cc}
1 & 2 \\
3 & 4 \\
\end{array}
\]
\[
\begin{array}{cc}
1 & 3 \\
2 & 4 \\
\end{array}
\]
Let \( C_n \) denote the number of standard tableau of shape \( 2 \times n \). Compute \( C_1, C_2, C_3, \) and \( C_4 \).
d. Prove that for all \( n \geq 1 \), \( A_n = B_n = C_n \). Hint: Find explicit bijective functions among the set of lattice paths that do not pass above the diagonal \( y = x \), the set of correctly matched parentheses, and the set of standard tableaux of shape \( 2 \times n \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F7a51d15d-a9a3-449d-a2a2-e3bf35bb9007%2F7fb9f1eb-b737-4404-bb38-94014094148c%2Fx8vifw_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Set on Combinatorics**
a. Let \( A_n \) denote the number of lattice paths from \((0, 0)\) to \((n, n)\) that do not pass above the diagonal \( y = x \). Find \( A_1, A_2, A_3, \) and \( A_4 \).
b. Let \( B_n \) denote the number of expressions containing \( n \) pairs of parentheses which are correctly matched. For example, \( B_2 = 2 \), since \(()() \) and \( (()) \) are the only two sets of correctly matched parentheses. Compute \( B_1, B_2, B_3, \) and \( B_4 \).
c. A **standard tableau** of shape \( 2 \times n \) is a \( 2 \times n \)-grid filled with the numbers 1, 2, \ldots, 2n, using each number once, so that every row increases left to right and every column increases top to bottom. For example, there are 2 standard tableaux of shape \( 2 \times 2 \):
\[
\begin{array}{cc}
1 & 2 \\
3 & 4 \\
\end{array}
\]
\[
\begin{array}{cc}
1 & 3 \\
2 & 4 \\
\end{array}
\]
Let \( C_n \) denote the number of standard tableau of shape \( 2 \times n \). Compute \( C_1, C_2, C_3, \) and \( C_4 \).
d. Prove that for all \( n \geq 1 \), \( A_n = B_n = C_n \). Hint: Find explicit bijective functions among the set of lattice paths that do not pass above the diagonal \( y = x \), the set of correctly matched parentheses, and the set of standard tableaux of shape \( 2 \times n \).
Expert Solution
Step 1
As per the norms, we will be answering the first question. If you need an answer to others, then kindly re-post the question by specifying it.
For (a),
Let us denote to be the number of lattice paths from (0, 0) to (n, n) that do not pass above the diagonal .
Now, we need to find .
For :
Here, is the number of lattice paths from (0, 0) to (1, 1) that do not pass above the diagonal .
So, we get the following.
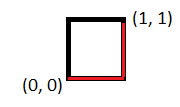
Thus, we have .
Step by step
Solved in 4 steps with 8 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

