kt Find an exponential function of the form P(t)=yoe to model the given data. In 1985, the number of female athletes participating in Summer Olympic-Type Games was 550. In 1996, about 3,600 participated in the Summer Olympics-Type games. Assuming that P(0) = 550 and that the exponential model applies, find the value of k rounded to the hundredths place, and write the function. A. k=0.19; P(t) = 550e 0.19t B. k= 0.27; P(t) = 550e 0.27t OC. k= 0.16; P(t) = 550 e 0.16t O D. k= 0.17; P(t) = 550 e 0.17t
kt Find an exponential function of the form P(t)=yoe to model the given data. In 1985, the number of female athletes participating in Summer Olympic-Type Games was 550. In 1996, about 3,600 participated in the Summer Olympics-Type games. Assuming that P(0) = 550 and that the exponential model applies, find the value of k rounded to the hundredths place, and write the function. A. k=0.19; P(t) = 550e 0.19t B. k= 0.27; P(t) = 550e 0.27t OC. k= 0.16; P(t) = 550 e 0.16t O D. k= 0.17; P(t) = 550 e 0.17t
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:**Exploring Exponential Growth in Athletics Participation**
**Analyzing Growth Models:**
In the context of modeling participation in the Summer Olympic-Type Games, we aim to establish an exponential function of the form \( P(t) = y_0 e^{kt} \).
**Historical Data:**
- **1985:** 550 female athletes participated.
- **1996:** The number increased to approximately 3,600 participants.
**Objective:**
Determine the growth rate constant \( k \) and write the exponential function, given that \( P(0) = 550 \). The calculations should round \( k \) to the nearest hundredth.
**Options for \( k \):**
A. \( k = 0.19 \); \( P(t) = 550e^{0.19t} \)
B. \( k = 0.27 \); \( P(t) = 550e^{0.27t} \)
C. \( k = 0.16 \); \( P(t) = 550e^{0.16t} \)
D. \( k = 0.17 \); \( P(t) = 550e^{0.17t} \)
To solve, evaluate these options to find the correct exponential growth rate that aligns with the historical data.
Expert Solution
Step 1
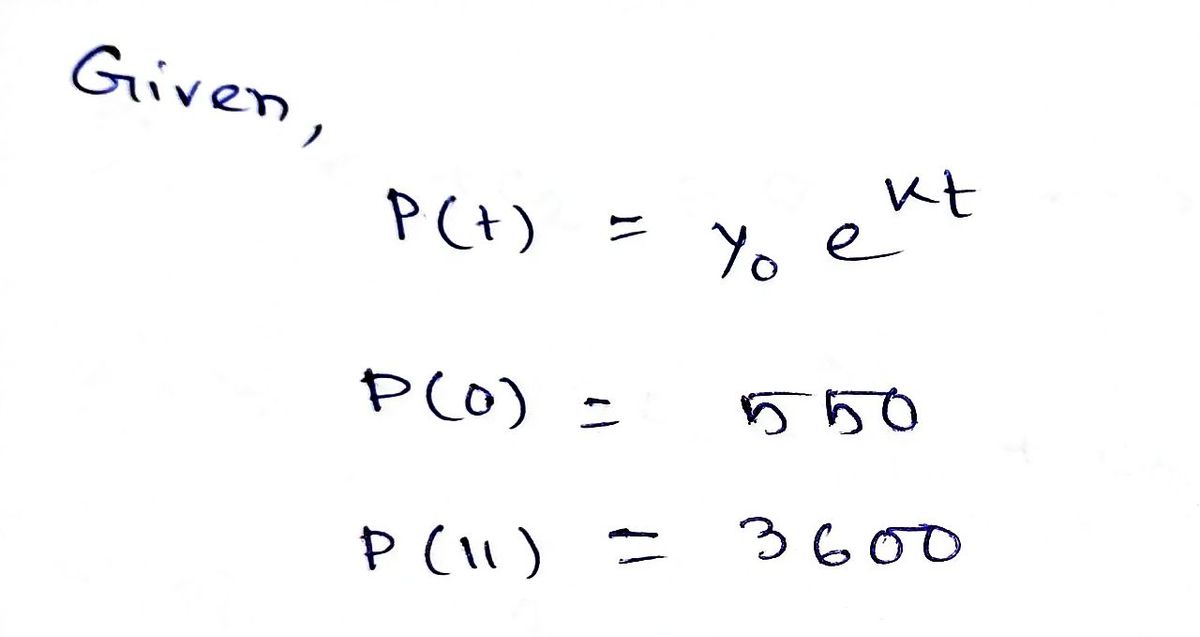
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

