konsider the conditon atbtetd =l, aud these equators + d = 279 -.05b 156+.10c +old = 0 + ,0 2b +,08b +05C a 40a Ic 10 a e15a 25c +old = 0 - .02d3D0 %3D use Gauss hrdan's Methad to Solve tue abore
Permutations and Combinations
If there are 5 dishes, they can be relished in any order at a time. In permutation, it should be in a particular order. In combination, the order does not matter. Take 3 letters a, b, and c. The possible ways of pairing any two letters are ab, bc, ac, ba, cb and ca. It is in a particular order. So, this can be called the permutation of a, b, and c. But if the order does not matter then ab is the same as ba. Similarly, bc is the same as cb and ac is the same as ca. Here the list has ab, bc, and ac alone. This can be called the combination of a, b, and c.
Counting Theory
The fundamental counting principle is a rule that is used to count the total number of possible outcomes in a given situation.
Please see attached question. Thanks for your help!
![**Systems of Equations and Gauss-Jordan Elimination**
**Consider the condition \( a + b + c + d = 1 \), and these equations:**
\[ a + b + c + d = 1 \]
\[ 0.4a - 0.05b - 0.1c = 0 \]
\[ 0.15a - 0.15b + 0.1c + 0.1d = 0 \]
\[ 0.1a + 0.02b - 0.25c + 0.1d = 0 \]
\[ 0.15a + 0.08b + 0.05c - 0.02d = 0 \]
**Use Gauss-Jordan's Method to solve the above equations.**
These equations represent a system of linear equations in four variables \(a\), \(b\), \(c\), and \(d\). To solve them using Gauss-Jordan elimination, we will need to transform the system into its reduced row-echelon form. This method involves performing row operations on the augmented matrix of the system until each leading coefficient is 1 and each column containing a leading 1 has zeros everywhere else.
1. **Write the augmented matrix** from the system of equations.
2. **Perform row operations** to reach the reduced row-echelon form.
3. **Solve for the variables** \(a\), \(b\), \(c\), and \(d\).
This step-by-step approach helps in understanding the interrelation between the equations and simplifies solving for multiple unknowns effectively.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F4e80d594-14a8-4713-8ea5-1fda205a6b86%2F8caf8e00-eb33-4a91-b5bf-1be3a82c57c0%2Fzda8uae.png&w=3840&q=75)
We are given the equations,
a + b + c + d = 1, ----------(1)
0.40a - 0.05b - 0.1c = 0 ---------(2)
0.15a - 0.15b - 0.10c + 0.1d = 0 ----------(3)
0.10a + 0.02b - 0.25c + 0.1d = 0 ---------(4)
0.15a + 0.08b + 0.05c - 0.02d = 0. --------(5)
Now, (2)x100, (3)x100, (4)x100, and (5)x100. Then new from of quation becomes,
a + b + c + d = 1, ----------(1)
40a - 5b - 10c = 0 ---------(2)
15a - 15b - 10c + 10d = 0 ----------(3)
10a + 2b - 25c + 10d = 0 ---------(4)
15a + 8b + 5c - 2d = 0. --------(5)
So, in the matrix form,
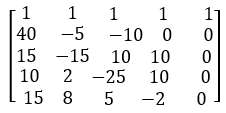 .
.
Now, we will be solving by Gauss Jordan's method.




Step by step
Solved in 6 steps with 15 images









