Kari requests two goods: X and Y. The utility function is given by: U(XY)=X-Y. Prices of X and Y is Px and Py, and budget is of m dollars. a) Deduce Karis demand for good X and Y b) Suggest price X and Y is showed by Px = 4 and Py = 2 and income, M, is 30. How much will she demand of X and Y? c) Karis wage is doubled. How does this affect her adjustment? Show graphically and mathematically d) is good X and Y normal or inferior goods?
Kari requests two goods: X and Y.
The utility function is given by: U(XY)=X-Y. Prices of X and Y is Px and Py, and budget is of m dollars.
a) Deduce Karis
b) Suggest
c) Karis wage is doubled. How does this affect her adjustment? Show graphically and mathematically
d) is good X and Y normal or inferior goods?
a)
Note that utility function U(X, Y) = X-Y is decreasing in Y. That is, increasing consumption of Y decreases Kari's utility.
Now suppose we are at the indifference curve (IC) which gives a utility of 10. So, the equation of this indifference curve is
X-Y=10. Note that the bundles (X=10, Y=0), (X=12, Y=2), (X=16, Y=6) are all on the same IC. Since both X and Y have positive prices, utility of 10 is achieved at the least cost when X = 10 and Y = 0.
This holds true in general as well. The ICs are given by equations of the form X-Y=U0 for varying values of U0. Note that these are all upward sloping, and ICs giving higher utilities are those which are more to the right (or have higher x intercept). Then, given the budget line (red line below), note that the highest IC which can be reached is the one which intersects the budget line at the x-axis.
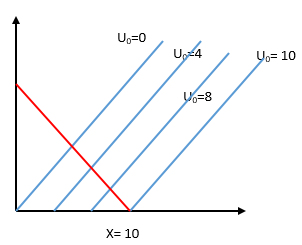
So the entire income will always be spent on good X and demand for Y is always Y=0
Hence, demand is X=m/Px and Y=0
Step by step
Solved in 4 steps with 2 images









