IV. Two integers x and y are said to be of the same parity if x and y are both even or are both odd. The integers x and y are of opposite parity if one of x and y is even and the other is odd. For example, 5 and 13 have the same parity while 8 and 11 are of opposite parity. a. Prove that for all integers x and y, if 41(x² − y²) then x and y have the same parity. - b. State and prove the converse of "part a" of this problem.
IV. Two integers x and y are said to be of the same parity if x and y are both even or are both odd. The integers x and y are of opposite parity if one of x and y is even and the other is odd. For example, 5 and 13 have the same parity while 8 and 11 are of opposite parity. a. Prove that for all integers x and y, if 41(x² − y²) then x and y have the same parity. - b. State and prove the converse of "part a" of this problem.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
100%
Please write a formal and well written proof for the following question...

Transcribed Image Text:**IV. Parity of Integers**
Two integers \( x \) and \( y \) are said to be of the **same parity** if \( x \) and \( y \) are both even or are both odd. The integers \( x \) and \( y \) are of **opposite parity** if one of \( x \) and \( y \) is even and the other is odd. For example, 5 and 13 have the same parity, while 8 and 11 are of opposite parity.
a. Prove that for all integers \( x \) and \( y \), if \( 4 \mid (x^2 - y^2) \), then \( x \) and \( y \) have the same parity.
b. State and prove the converse of "part a" of this problem.
Expert Solution
Step 1: Part a

Step by step
Solved in 3 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Can you re-explain how you did the cases like you did and why they prove they'll always be the same parity for part a as I do not understand it...
Original Question:
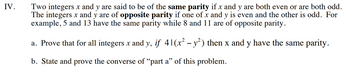
Transcribed Image Text:IV.
Two integers x and y are said to be of the same parity if x and y are both even or are both odd.
The integers x and y are of opposite parity if one of x and y is even and the other is odd. For
example, 5 and 13 have the same parity while 8 and 11 are of opposite parity.
a. Prove that for all integers x and y, if 41(x² − y²) then x and y have the same parity.
b. State and prove the converse of "part a" of this problem.
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

