It costs a baker a fixed cost of $420 and variable cost of $2.10 per cupcake. A cupcake is sold for $4.90 each.(iii) Write an algebraic expression representing the cost C as a function of the number of cupcakes x that are produced.(iv) Write an algebraic expression representing the revenue R as a function of the number of cupcakes x sold.(v) Graph both functions on the same coordinate axes.(vi) From your graph find coordinatae at which cost equals revenue.(vii) Using your graph, determine how many cupcakes need to be made to produce revenue of at least $1,029.How much profit is made for this number of cupcakes? ANSWER (vi) AND (vii) ONLY
Rate of Change
The relation between two quantities which displays how much greater one quantity is than another is called ratio.
Slope
The change in the vertical distances is known as the rise and the change in the horizontal distances is known as the run. So, the rise divided by run is nothing but a slope value. It is calculated with simple algebraic equations as:
It costs a baker a fixed cost of $420 and variable cost of $2.10 per cupcake. A cupcake is sold for $4.90 each.
(iii) Write an algebraic expression representing the cost C as a function of the number of cupcakes x that are produced.
(iv) Write an algebraic expression representing the revenue R as a function of the number of cupcakes x sold.
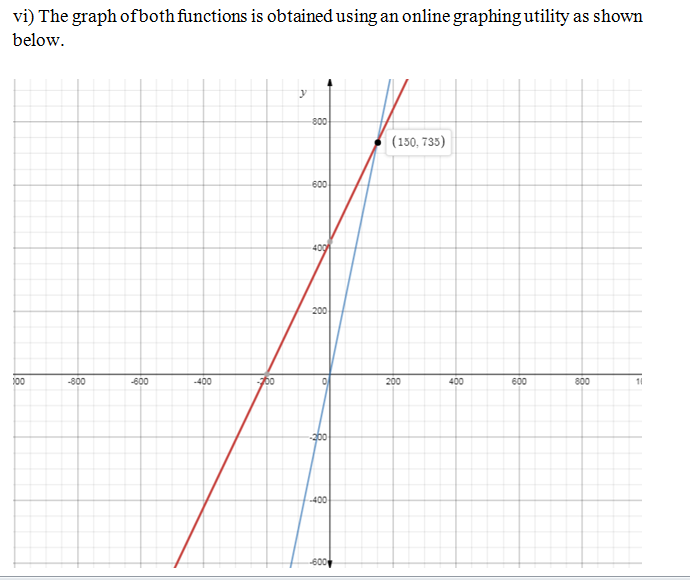
(v) Graph both functions on the same coordinate axes.
(vi) From your graph find coordinatae at which cost equals revenue.
(vii) Using your graph, determine how many cupcakes need to be made to produce revenue of at least $1,029.How much profit is made for this number of cupcakes?
ANSWER (vi) AND (vii) ONLY

Step by step
Solved in 5 steps with 5 images









