Lizards of a valuable breed (Alligator lizards) have been introduced onto Lizard Island and their population is growing. The Population (P) is modelled by the differential equation dp/pt=-k(p-m) where t is the number of years that have passed since January 2022, M is an upper bound on the population due to limitations on the island’s natural resources, and k is a constant relating to the net population growth rate. Customers (Paying tourists) of the island seeing some lizards is essential for the business, so the operator is keen for the number of lizards to reach 75% of M in January 2028 (a) Use the separation of variables technique to formulate a solution to the differential equation. (b) In January 2022, there were 50 lizards and in January 2023 there were 60. Current scientific research estimates k as 0.05, but M is unknown. Estimate M from this data. (c) The business wants to start feeding the lizards vitamins from January 2023 to help increase the value of k. Vitamins are expensive, so the business wants to know the minimal value of k required to bring the lizard population to the target. Determine the minimal value of k to achieve the target after observing the January 2023 data.
I need some help, Also can you show me all the steps, please?
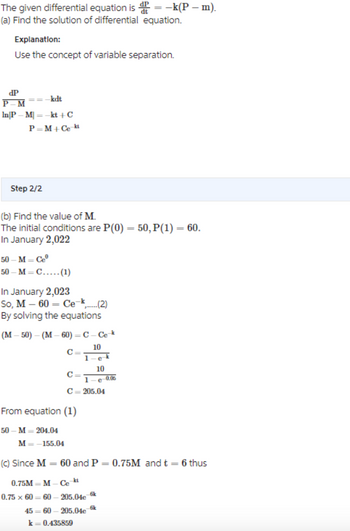
Lizards of a valuable breed (Alligator lizards) have been introduced onto Lizard Island and their population is growing. The Population (P) is modelled by the differential equation dp/pt=-k(p-m) where t is the number of years that have passed since January 2022, M is an upper bound on the population due to limitations on the island’s natural resources, and k is a constant relating to the net population growth rate. Customers (Paying tourists) of the island seeing some lizards is essential for the business, so the operator is keen for the number of lizards to reach 75% of M in January 2028
(a) Use the separation of variables technique to formulate a solution to the differential equation.
(b) In January 2022, there were 50 lizards and in January 2023 there were 60. Current scientific research estimates k as 0.05, but M is unknown. Estimate M from this data.
(c) The business wants to start feeding the lizards vitamins from January 2023 to help increase the value of k. Vitamins are expensive, so the business wants to know the minimal value of k required to bring the lizard population to the target. Determine the minimal value of k to achieve the target after observing the January 2023 data.
Step by step
Solved in 4 steps with 6 images

Is this right or wrong