IQ is normally distributed with a mean of 100 (SD = 15). What score would a person need to be in the top 17% of scores? What score would separate the lowest 67% of scores from the highest 33%? What score separates the highest 2% of IQ?
Continuous Probability Distributions
Probability distributions are of two types, which are continuous probability distributions and discrete probability distributions. A continuous probability distribution contains an infinite number of values. For example, if time is infinite: you could count from 0 to a trillion seconds, billion seconds, so on indefinitely. A discrete probability distribution consists of only a countable set of possible values.
Normal Distribution
Suppose we had to design a bathroom weighing scale, how would we decide what should be the range of the weighing machine? Would we take the highest recorded human weight in history and use that as the upper limit for our weighing scale? This may not be a great idea as the sensitivity of the scale would get reduced if the range is too large. At the same time, if we keep the upper limit too low, it may not be usable for a large percentage of the population!
- IQ is
normally distributed with amean of 100 (SD = 15).- What score would a person need to be in the top 17% of scores?
- What score would separate the lowest 67% of scores from the highest 33%?
- What score separates the highest 2% of IQ?
Let X denote the IQ scores and it follows normal distribution with mean of 100 and standard deviation of 15
(1)
The score would a person need to be in the top 17% of scores is,
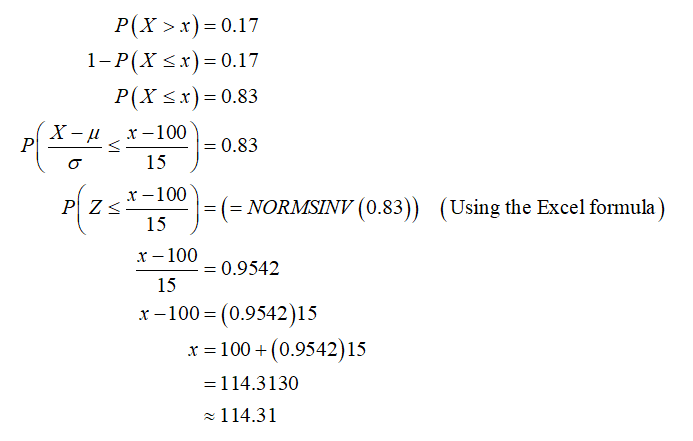
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images









