Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Integrate: 14 9x²+2x-1 (x-1)(2x²+7x-4) dx

Integrate: 14 9x²+2x-1 (x-1)(2x²+7x-4) dx

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question

Solve it by Partial Fraction

**Integrate:** \[ \int_{2}^{14} \frac{9x^2 + 2x - 1}{(x-1)(2x^2 + 7x - 4)} \, dx \] This integral involves a rational function, where the numerator is a polynomial \(9x^2 + 2x - 1\) and the denominator is a product of polynomials \((x-1)(2x^2 + 7x - 4)\). The definite integral is evaluated from \(x = 2\) to \(x = 14\). This type of problem typically requires partial fraction decomposition to simplify the integrand before integrating.
Transcribed Image Text:**Integrate:** \[ \int_{2}^{14} \frac{9x^2 + 2x - 1}{(x-1)(2x^2 + 7x - 4)} \, dx \] This integral involves a rational function, where the numerator is a polynomial \(9x^2 + 2x - 1\) and the denominator is a product of polynomials \((x-1)(2x^2 + 7x - 4)\). The definite integral is evaluated from \(x = 2\) to \(x = 14\). This type of problem typically requires partial fraction decomposition to simplify the integrand before integrating.
Expert Solution
Step 1

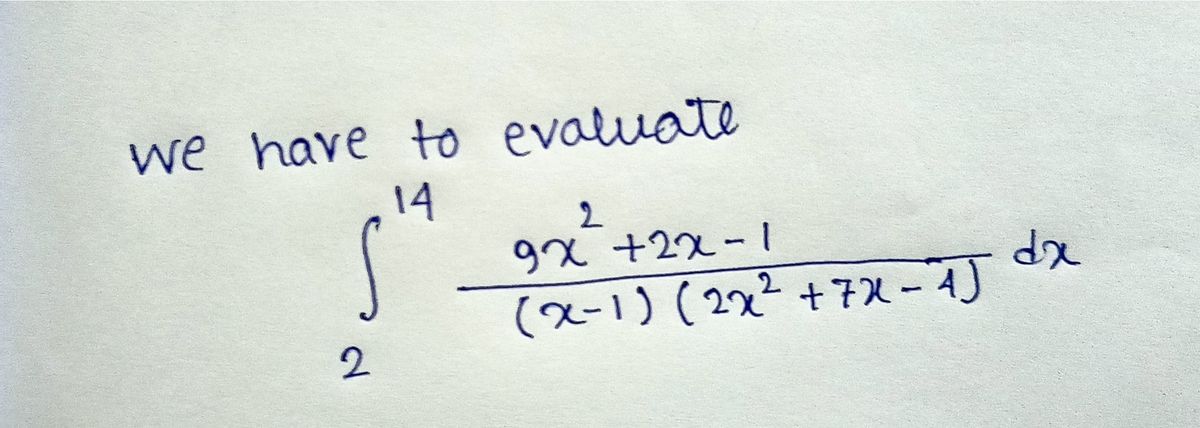
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS