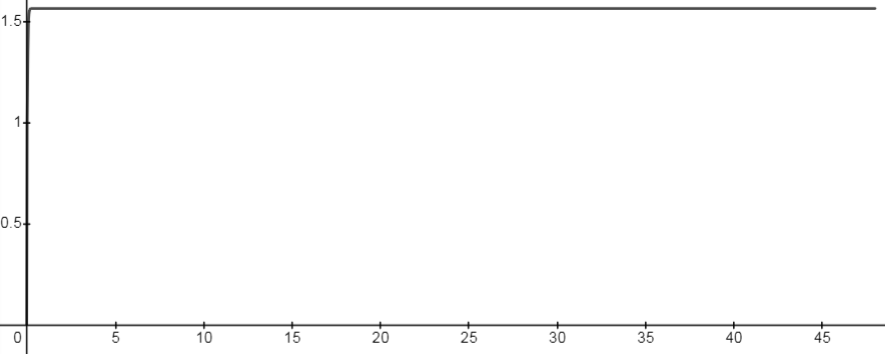
Infusion: An IV line provides a continuous flow of a drug directly into the bloodstream. Assuming A no initial drug presence, the amount of the drug aftert hours is given by m(t) = ÷ (1 – e-kt) for t > 0, where A is the rate the drug flows in milligrams per hour. We say the steady state level is the amount of drug remaining after a long time has passed. k 1. Suppose an antibiotic with a half-life of 12 hours is given intravenously with A = 50 . Find the rate constant k and graph m(t) for 0
Cylinders
A cylinder is a three-dimensional solid shape with two parallel and congruent circular bases, joined by a curved surface at a fixed distance. A cylinder has an infinite curvilinear surface.
Cones
A cone is a three-dimensional solid shape having a flat base and a pointed edge at the top. The flat base of the cone tapers smoothly to form the pointed edge known as the apex. The flat base of the cone can either be circular or elliptical. A cone is drawn by joining the apex to all points on the base, using segments, lines, or half-lines, provided that the apex and the base both are in different planes.
4. m(t) = 400e^-0.462t

From question 4, we have .
Here, the amount of drug after t hours is .
The half life is 12 hours and .
So,
Use this amount and obtain the value of k:
The value of k is 31.969.
The amount of drug after t hours is .
The graph of m is obtained as shown below:
Step by step
Solved in 3 steps with 1 images









