Indicate the values of x and y such that the following equation holds for every sequence {an}n>0 60 60 Σπο an - Στο απ 44 από = 20 am 2= = y= =y απ
Indicate the values of x and y such that the following equation holds for every sequence {an}n>0 60 60 Σπο an - Στο απ 44 από = 20 am 2= = y= =y απ
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Title: Finding Values of x and y in a Summation Equation**
**Objective:** Determine the values of \( x \) and \( y \) such that the given equation holds true for any sequence \(\{ a_n \}_{n \geq 0} \).
**Equation:**
\[
\sum_{n=20}^{44} a_n = \sum_{n=0}^{60} a_n - \sum_{m=0}^{x} a_n - \sum_{n=y}^{60} a_n
\]
**Inputs:**
- **x =** [Input Box]
- **y =** [Input Box]
**Instructions:**
1. Identify and simplify the given equation by considering the ranges of indices in the summations.
2. Recognize boundaries for values of \( n \) in different summations and relate values \( x \) and \( y \) to these boundaries to ensure equality.
**Note:** The solution may require solving for conditions under which the series on both sides of the equation are equal by balancing the terms.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3632b9ca-0e22-48c8-943d-c9e08fc0f04c%2Fd29d776d-ba33-40ee-8372-c84e4262c3eb%2F9i5zqo_processed.png&w=3840&q=75)
Transcribed Image Text:**Title: Finding Values of x and y in a Summation Equation**
**Objective:** Determine the values of \( x \) and \( y \) such that the given equation holds true for any sequence \(\{ a_n \}_{n \geq 0} \).
**Equation:**
\[
\sum_{n=20}^{44} a_n = \sum_{n=0}^{60} a_n - \sum_{m=0}^{x} a_n - \sum_{n=y}^{60} a_n
\]
**Inputs:**
- **x =** [Input Box]
- **y =** [Input Box]
**Instructions:**
1. Identify and simplify the given equation by considering the ranges of indices in the summations.
2. Recognize boundaries for values of \( n \) in different summations and relate values \( x \) and \( y \) to these boundaries to ensure equality.
**Note:** The solution may require solving for conditions under which the series on both sides of the equation are equal by balancing the terms.
Expert Solution
Step 1
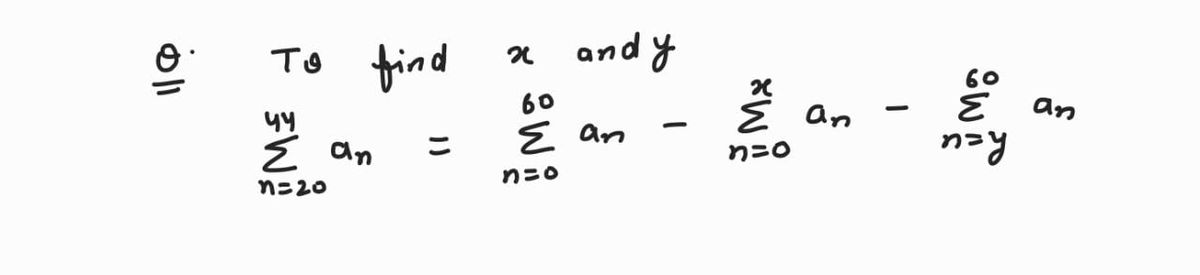
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

