In this problem we consider an equation in differential form M da + N dy = 0. The equation (20z*y'e- 2e* sin(x) + 3e ) dx + (20x'y'e 9e 3)dy 0 in differential form M dx +N dy = 0 is not exact. Indeed, we have M,- N. For this exercise we can find an integrating factor which is a function of x alone since M,- N, N can be considered as a function of x alone. Namely we have µ(x) %3D Multiplying the original equation by the integrating factor we obtain a new equation M dx + N dy = 0 where M = N = Which is exact since My N =
In this problem we consider an equation in differential form M da + N dy = 0. The equation (20z*y'e- 2e* sin(x) + 3e ) dx + (20x'y'e 9e 3)dy 0 in differential form M dx +N dy = 0 is not exact. Indeed, we have M,- N. For this exercise we can find an integrating factor which is a function of x alone since M,- N, N can be considered as a function of x alone. Namely we have µ(x) %3D Multiplying the original equation by the integrating factor we obtain a new equation M dx + N dy = 0 where M = N = Which is exact since My N =
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![In this problem, we consider an equation in differential form \( M \, dx + N \, dy = 0 \).
The equation
\[
(20x^4y^5e^{-x} - 2e^{-x} \sin(x) + 3e^{-3y}) \, dx + (20x^5y^4e^{-x} - 9e^{-3y}) \, dy = 0
\]
in differential form \( M \, dx + N \, dy = 0 \) is not exact. Indeed, we have
\[
\bar{M}_y - \bar{N}_x =
\]
For this exercise, we can find an integrating factor which is a function of \( x \) alone since
\[
\frac{\bar{M}_y - \bar{N}_x}{N} =
\]
can be considered as a function of \( x \) alone.
Namely, we have \( \mu(x) = \)
Multiplying the original equation by the integrating factor, we obtain a new equation \( M \, dx + N \, dy = 0 \) where
\[
M =
\]
\[
N =
\]
which is exact since
\[
M_y =
\]
\[
N_x =
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0b6335cc-d6e6-4edb-a931-307e282480f3%2F01ba1c77-e52a-491a-b83a-e3e1f69001ca%2Fxmt04o_processed.jpeg&w=3840&q=75)
Transcribed Image Text:In this problem, we consider an equation in differential form \( M \, dx + N \, dy = 0 \).
The equation
\[
(20x^4y^5e^{-x} - 2e^{-x} \sin(x) + 3e^{-3y}) \, dx + (20x^5y^4e^{-x} - 9e^{-3y}) \, dy = 0
\]
in differential form \( M \, dx + N \, dy = 0 \) is not exact. Indeed, we have
\[
\bar{M}_y - \bar{N}_x =
\]
For this exercise, we can find an integrating factor which is a function of \( x \) alone since
\[
\frac{\bar{M}_y - \bar{N}_x}{N} =
\]
can be considered as a function of \( x \) alone.
Namely, we have \( \mu(x) = \)
Multiplying the original equation by the integrating factor, we obtain a new equation \( M \, dx + N \, dy = 0 \) where
\[
M =
\]
\[
N =
\]
which is exact since
\[
M_y =
\]
\[
N_x =
\]

Transcribed Image Text:The text on the image is as follows:
---
\( N_x = \)
are equal.
This problem is exact. Therefore, an implicit general solution can be written in the form \( F(x, y) = C \) where
\( F(x, y) = \)
---
There are no graphs or diagrams in the image.
Expert Solution
Step 1
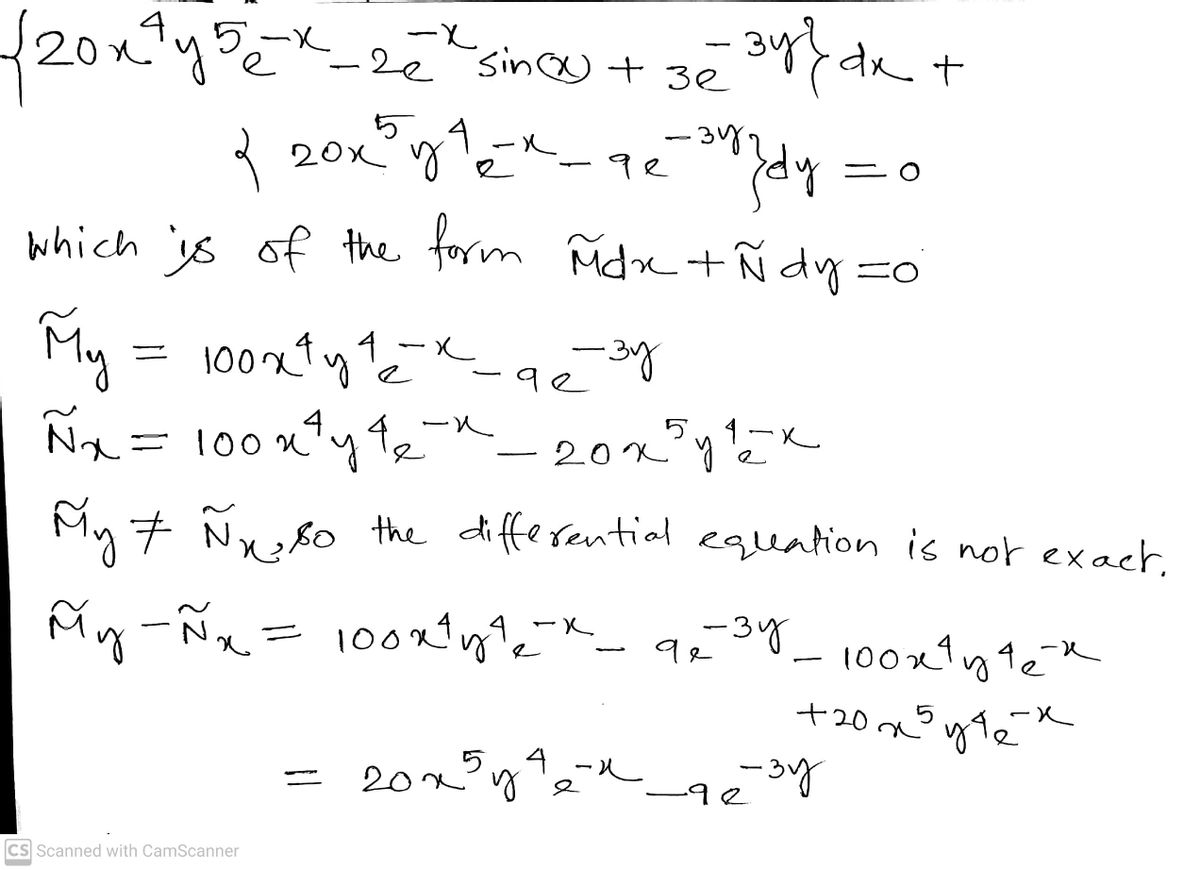
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

