Given an undirected weighted graph G with n nodes and m edges, and we have used Prim’s algorithm to construct a minimum spanning tree T. Suppose the weight of one of the tree edge ((u, v) ∈ T) is changed from w to w′, design an algorithm to verify whether T is still a minimum spanning tree. Your algorithm should run in O(m) time, and explain why your algorithm is correct. You can assume all the weights are distinct. (Hint: When an edge is removed, nodes of T will break into two groups. Which edge should we choose in the cut of these two groups?)
Given an undirected weighted graph G with n nodes and m edges, and we have used Prim’s
Trending now
This is a popular solution!
Step by step
Solved in 2 steps

In the following
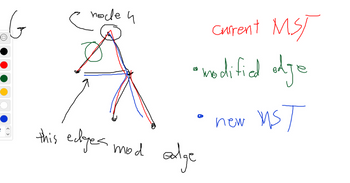
If we run Prim's again in step 2, that would merit a mlogn runtime not m runtime. Is there an alternative to this








