In Exercises 16-19, prove the given property of the Fibonacci numbers for all n ≥ 1. (Hint: The first principle of induction will work.)
In Exercises 16-19, prove the given property of the Fibonacci numbers for all n ≥ 1. (Hint: The first principle of induction will work.)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Fibonacci Sequence Identities
Here are some interesting identities related to the Fibonacci sequence:
17. \( F(2) + F(4) + \ldots + F(2n) = F(2n + 1) - 1 \)
This identity represents the sum of every second Fibonacci number starting from \( F(2) \) up to \( F(2n) \). The sum is equal to the Fibonacci number at position \( 2n + 1 \), minus one.
18. \( F(1) + F(3) + \ldots + F(2n - 1) = F(2n) \)
This identity indicates that the sum of every second Fibonacci number starting from \( F(1) \) up to \( F(2n - 1) \) equals the Fibonacci number at position \( 2n \).
19. \( [F(1)]^2 + [F(2)]^2 + \ldots + [F(n)]^2 = F(n)F(n + 1) \)
This identity shows that the sum of the squares of the first \( n \) Fibonacci numbers is equal to the product of the Fibonacci number at position \( n \) and the Fibonacci number at position \( n + 1 \).
These identities can be useful in mathematical theory and applications involving the Fibonacci sequence.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F000774e1-5c4d-48f4-ab3a-32fc5a27d75a%2F0e0393ad-3a16-4238-aab9-393d5f60f097%2Fakk3cip_processed.png&w=3840&q=75)
Transcribed Image Text:### Fibonacci Sequence Identities
Here are some interesting identities related to the Fibonacci sequence:
17. \( F(2) + F(4) + \ldots + F(2n) = F(2n + 1) - 1 \)
This identity represents the sum of every second Fibonacci number starting from \( F(2) \) up to \( F(2n) \). The sum is equal to the Fibonacci number at position \( 2n + 1 \), minus one.
18. \( F(1) + F(3) + \ldots + F(2n - 1) = F(2n) \)
This identity indicates that the sum of every second Fibonacci number starting from \( F(1) \) up to \( F(2n - 1) \) equals the Fibonacci number at position \( 2n \).
19. \( [F(1)]^2 + [F(2)]^2 + \ldots + [F(n)]^2 = F(n)F(n + 1) \)
This identity shows that the sum of the squares of the first \( n \) Fibonacci numbers is equal to the product of the Fibonacci number at position \( n \) and the Fibonacci number at position \( n + 1 \).
These identities can be useful in mathematical theory and applications involving the Fibonacci sequence.

Transcribed Image Text:In Exercises 16–19, prove the given property of the Fibonacci numbers for all \( n \geq 1 \). (Hint: The first principle of induction will work.)
Expert Solution
Step 1
Note: “Since you have posted a question with multiple sub-parts, we will solve first three subparts for you. To get remaining sub-part solved please repost the complete question and mention the sub-parts to be solved.”
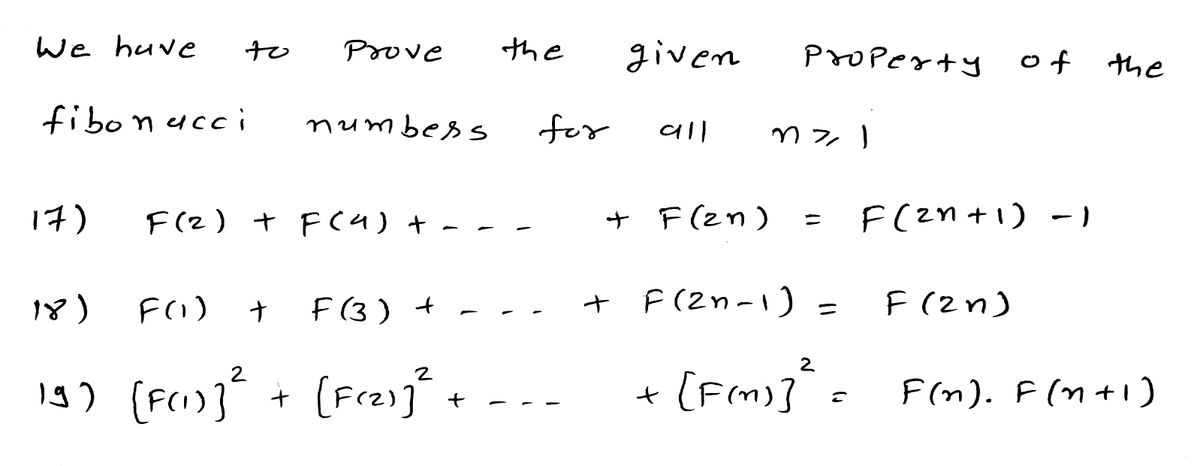
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 5 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

