Answered: In a country, the amount of lead in a…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Topic Video

Question

In a country, the amount of lead in a contained city's water supply is normally distributed with a mean of 30 micrograms/L and a standard deviation of 4 micrograms/L.

a)Suppose we collect samples from 16 different cities. Determine the probability that the sample mean will contain more than 31 micrograms/ L of lead.

b) After filtering lead, the true mean changes. A sample of 100 cities yield a sample mean of 20 micrograms/L of lead. Compute a 90% confidence interval for the new true mean amount of lead.

Definition Definition Measure of central tendency that is the average of a given data set. The mean value is evaluated as the quotient of the sum of all observations by the sample size. The mean, in contrast to a median, is affected by extreme values. Very large or very small values can distract the mean from the center of the data. Arithmetic mean: The most common type of mean is the arithmetic mean. It is evaluated using the formula: μ = 1 N ∑ i = 1 N x i Other types of means are the geometric mean, logarithmic mean, and harmonic mean. Geometric mean: The nth root of the product of n observations from a data set is defined as the geometric mean of the set: G = x 1 x 2 ... x n n Logarithmic mean: The difference of the natural logarithms of the two numbers, divided by the difference between the numbers is the logarithmic mean of the two numbers. The logarithmic mean is used particularly in heat transfer and mass transfer. ln x 2 − ln x 1 x 2 − x 1 Harmonic mean: The inverse of the arithmetic mean of the inverses of all the numbers in a data set is the harmonic mean of the data. 1 1 x 1 + 1 x 2 + ...

Expert Solution

Step 1

Solution:

Let X be the amount of lead in a contained city’s water supply.

From the given information, X follows normal distribution with mean µ=30 micrograms/L and a standard deviation σ=4 micrograms/L.

Step 2

The probability that the sample mean will contain more than 31 micrograms/L of lead is

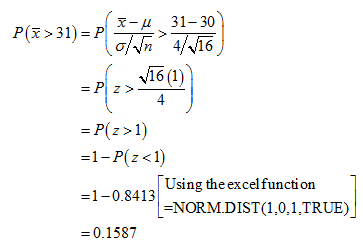
Thus, the probability that the sample mean will contain more than 31 micrograms/L of lead is 0.1587.

Step by step

Solved in 4 steps with 3 images

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Means$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Similar questions