If the V= 4.2x3yz+8xy“, calculate the x-component of the electric field at point (2.2,7,16.832) Round your answer to 2 decimal places.
If the V= 4.2x3yz+8xy“, calculate the x-component of the electric field at point (2.2,7,16.832) Round your answer to 2 decimal places.
Related questions
Question
![### Problem Statement
Given the potential function \( V = 4.2x^3 yz + 8xy^4 \), calculate the x-component of the electric field at the point \( (2.2, 7, 16.83) \).
Round your answer to 2 decimal places.
### Solution
To find the x-component of the electric field, \( E_x \), we need to take the negative partial derivative of the potential function \( V \) with respect to \( x \):
\[ E_x = -\frac{\partial V}{\partial x} \]
First, let's compute the partial derivative of \( V \):
\[ V = 4.2x^3 yz + 8xy^4 \]
\[ \frac{\partial V}{\partial x} = \frac{\partial}{\partial x} (4.2x^3 yz) + \frac{\partial}{\partial x} (8xy^4) \]
The first term:
\[ \frac{\partial}{\partial x} (4.2x^3 yz) = 4.2 \cdot 3x^2 yz = 12.6x^2 yz \]
The second term:
\[ \frac{\partial}{\partial x} (8xy^4) = 8y^4 \]
Now, adding these partial derivatives:
\[ \frac{\partial V}{\partial x} = 12.6x^2 yz + 8y^4 \]
Next, let's substitute the point \( (2.2, 7, 16.83) \) into this expression:
\[ \frac{\partial V}{\partial x} = 12.6 \cdot (2.2)^2 \cdot 7 \cdot 16.83 + 8 \cdot (7)^4 \]
Calculate each term separately:
1. \( (2.2)^2 = 4.84 \)
2. \( 12.6 \cdot 4.84 \cdot 7 \cdot 16.83 = 7134.16 \)
3. \( (7)^4 = 2401 \)
4. \( 8 \cdot 2401 = 19208 \)
Then, sum the results:
\[ \frac{\partial V}{\partial x} = 7134.16 + 19208 =](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fd447342a-76d3-44af-918e-aa75820122eb%2Ff1957e74-4a82-4b43-8830-de6380558807%2F0s4i0qa.jpeg&w=3840&q=75)
Transcribed Image Text:### Problem Statement
Given the potential function \( V = 4.2x^3 yz + 8xy^4 \), calculate the x-component of the electric field at the point \( (2.2, 7, 16.83) \).
Round your answer to 2 decimal places.
### Solution
To find the x-component of the electric field, \( E_x \), we need to take the negative partial derivative of the potential function \( V \) with respect to \( x \):
\[ E_x = -\frac{\partial V}{\partial x} \]
First, let's compute the partial derivative of \( V \):
\[ V = 4.2x^3 yz + 8xy^4 \]
\[ \frac{\partial V}{\partial x} = \frac{\partial}{\partial x} (4.2x^3 yz) + \frac{\partial}{\partial x} (8xy^4) \]
The first term:
\[ \frac{\partial}{\partial x} (4.2x^3 yz) = 4.2 \cdot 3x^2 yz = 12.6x^2 yz \]
The second term:
\[ \frac{\partial}{\partial x} (8xy^4) = 8y^4 \]
Now, adding these partial derivatives:
\[ \frac{\partial V}{\partial x} = 12.6x^2 yz + 8y^4 \]
Next, let's substitute the point \( (2.2, 7, 16.83) \) into this expression:
\[ \frac{\partial V}{\partial x} = 12.6 \cdot (2.2)^2 \cdot 7 \cdot 16.83 + 8 \cdot (7)^4 \]
Calculate each term separately:
1. \( (2.2)^2 = 4.84 \)
2. \( 12.6 \cdot 4.84 \cdot 7 \cdot 16.83 = 7134.16 \)
3. \( (7)^4 = 2401 \)
4. \( 8 \cdot 2401 = 19208 \)
Then, sum the results:
\[ \frac{\partial V}{\partial x} = 7134.16 + 19208 =
Expert Solution
Step 1
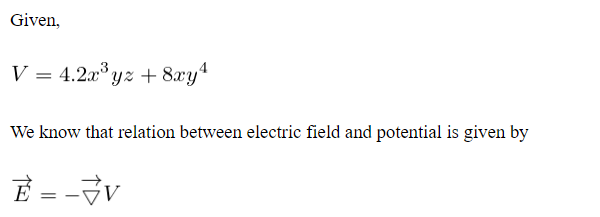
Step 2

Step by step
Solved in 3 steps with 3 images
