If the Accumulated Value of an investment at time t is AV₁ = 1.2+.1t², what is & when t=2? A. .05 B. .10 C. .15 D. .20 E. .25
If the Accumulated Value of an investment at time t is AV₁ = 1.2+.1t², what is & when t=2? A. .05 B. .10 C. .15 D. .20 E. .25
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
solve and give me explanation

Transcribed Image Text:**Problem Statement:**
If the Accumulated Value of an investment at time \( t \) is given by the formula \( AV_t = 1.2 + .1t^2 \), what is \( \delta_t \) when \( t = 2 \)?
**Options:**
A. 0.05
B. 0.10
C. 0.15
D. 0.20
E. 0.25
**Explanation:**
To solve this problem, you need to calculate the derivative of the accumulated value function to find the rate of change of the value at \( t = 2 \). The derivative of \( AV_t = 1.2 + .1t^2 \) with respect to \( t \) will help determine the instantaneous rate represented by \( \delta_t \). Remember to substitute \( t = 2 \) into the derivative to find \( \delta_t \).
Expert Solution
Step 1
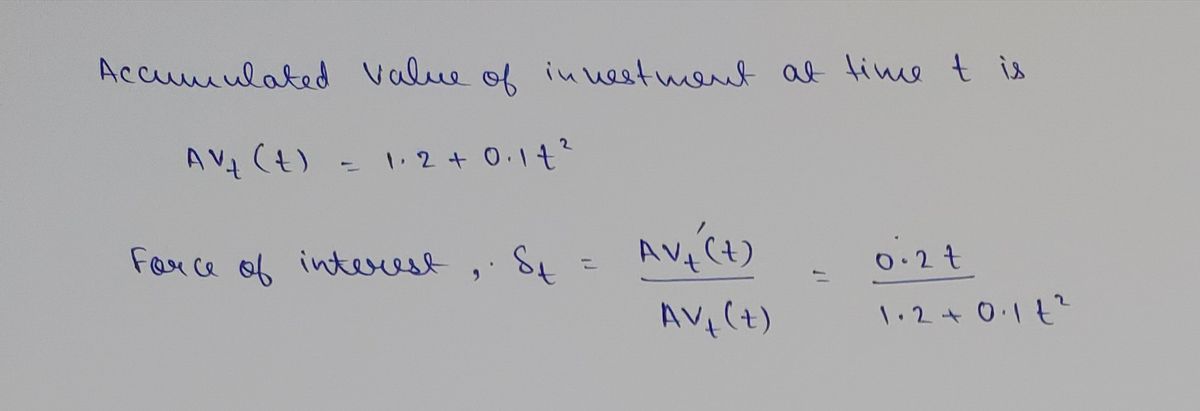
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

