Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![### Problem Statement
If \( f(x) = \frac{3 \tan x}{x} \), then:
1. \( f'(x) = \underline{\hspace{5cm}} \)
2. \( f'(4) = \underline{\hspace{5cm}} \)
### Explanation
This problem involves finding the derivative of the function \( f(x) = \frac{3 \tan x}{x} \) and then evaluating that derivative at \( x = 4 \).
To solve this:
1. Apply the quotient rule, which is used when finding the derivative of a function that is the quotient of two other functions: if \( g(x) = \frac{u(x)}{v(x)} \), then:
\[
g'(x) = \frac{u'(x)v(x) - u(x)v'(x)}{(v(x))^2}
\]
2. For \( f(x) = \frac{3 \tan x}{x} \), identify \( u(x) = 3 \tan x \) and \( v(x) = x \).
3. Calculate \( u'(x) \) and \( v'(x) \).
4. Substitute these into the quotient rule formula.
5. Evaluate \( f'(4) \) by substituting \( x = 4 \) into the derived expression for \( f'(x) \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F16b88384-b27c-4aea-b4d5-cecb5406683e%2F4605ad2c-ad22-4e56-82ba-639e2ae405d3%2Faqyal4k_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Problem Statement
If \( f(x) = \frac{3 \tan x}{x} \), then:
1. \( f'(x) = \underline{\hspace{5cm}} \)
2. \( f'(4) = \underline{\hspace{5cm}} \)
### Explanation
This problem involves finding the derivative of the function \( f(x) = \frac{3 \tan x}{x} \) and then evaluating that derivative at \( x = 4 \).
To solve this:
1. Apply the quotient rule, which is used when finding the derivative of a function that is the quotient of two other functions: if \( g(x) = \frac{u(x)}{v(x)} \), then:
\[
g'(x) = \frac{u'(x)v(x) - u(x)v'(x)}{(v(x))^2}
\]
2. For \( f(x) = \frac{3 \tan x}{x} \), identify \( u(x) = 3 \tan x \) and \( v(x) = x \).
3. Calculate \( u'(x) \) and \( v'(x) \).
4. Substitute these into the quotient rule formula.
5. Evaluate \( f'(4) \) by substituting \( x = 4 \) into the derived expression for \( f'(x) \).
Expert Solution
Step 1
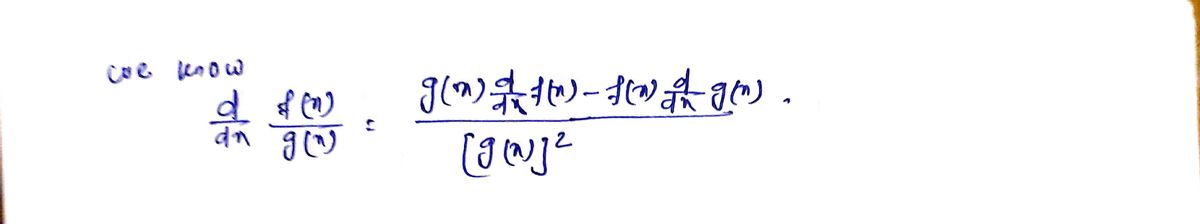
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning