ieN 6. (a) Uto, i+ 1] = (b) N[0,i+1]= ieN ieN 7. (a) URx[i,i+1] = (b) ORXlii+1l=
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Only 6b
![For any (a,b)ER,let
0}
ng set Pab) Consi
Indexed Sets
29
+by=0. From
that is, Pa,b) is a
automatically sa
Exercises for Section 1.8
1. Suppose A1 = {a,b,d,e,g.f}, A2 = {a,b,c,d}, As
(a,b,h).
(a) ỦA; =
(b)
3:x+233D0. It i
ex+2y 0.
A1
{0,2,4,8,10,12, 14, 16, 18,20,22,24},
2. Suppose
A2 = {0,3,6,9, 12, 15, 18,21,24},
A3
{0,4,8, 12, 16,20,24}.
(a) ỦA; =
(b)
i=1
3. For each nEN, let A, = {0, 1,2,3,...,n}.
(a) UA¡ =
(b) NA -
ieN
For each n EN, let A, = {-2n,0,2n}.
(a) UA =
(b) Ai
ieN
5. (a) Uli,i+1] =
(b) Nli,i+1]=
ieN
bian
ieN
(b) N[0,i +1] =
6. (a) Uto,i+ 1] =
ieN
ieN
nt ni s
7. (a) URX[i,i+1] =
(b) NR×[i,i+1]=
ieN
ieN
(b) N {a} × [0,1]=
ning the z-axis
8. (a) U{a} x [0,1] =
Joo acR
U X =
XeP(N)
(b) N X =
XeP(N)
9. (a)
alize P(a,b) as i
= 0. Figure l
s intersect aly
U [x, 1] x [0,x] =
(b)
xe[0,1]
n (x, 1) x [0, x1=
(10, (a)
xe[0,1]
t is immedit
11. Is NAa SUAq always true for any collection of sets Aa with index set I?
ael ael
12. If NAa =UAa, what do you think can be said about the relationships between
ael
the sets Aa?
13. If J#Ø and JcI, does it follow that U AaSUAq? What about N Aa sN Aa?
aEJ
ael
Ongs to thes
y 0, (Inat
aeJ
ael
only Pa
e have
aEJ
14, If J#Ø and JcI, does it follow that AasN Aa? Explain.
ael](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fd06cff55-e1fa-4bcb-ab93-6fc7f7940672%2Ff93771eb-692d-448e-8d15-d59a1370f51b%2F0me0lsr_processed.jpeg&w=3840&q=75)
Transcribed Image Text:For any (a,b)ER,let
0}
ng set Pab) Consi
Indexed Sets
29
+by=0. From
that is, Pa,b) is a
automatically sa
Exercises for Section 1.8
1. Suppose A1 = {a,b,d,e,g.f}, A2 = {a,b,c,d}, As
(a,b,h).
(a) ỦA; =
(b)
3:x+233D0. It i
ex+2y 0.
A1
{0,2,4,8,10,12, 14, 16, 18,20,22,24},
2. Suppose
A2 = {0,3,6,9, 12, 15, 18,21,24},
A3
{0,4,8, 12, 16,20,24}.
(a) ỦA; =
(b)
i=1
3. For each nEN, let A, = {0, 1,2,3,...,n}.
(a) UA¡ =
(b) NA -
ieN
For each n EN, let A, = {-2n,0,2n}.
(a) UA =
(b) Ai
ieN
5. (a) Uli,i+1] =
(b) Nli,i+1]=
ieN
bian
ieN
(b) N[0,i +1] =
6. (a) Uto,i+ 1] =
ieN
ieN
nt ni s
7. (a) URX[i,i+1] =
(b) NR×[i,i+1]=
ieN
ieN
(b) N {a} × [0,1]=
ning the z-axis
8. (a) U{a} x [0,1] =
Joo acR
U X =
XeP(N)
(b) N X =
XeP(N)
9. (a)
alize P(a,b) as i
= 0. Figure l
s intersect aly
U [x, 1] x [0,x] =
(b)
xe[0,1]
n (x, 1) x [0, x1=
(10, (a)
xe[0,1]
t is immedit
11. Is NAa SUAq always true for any collection of sets Aa with index set I?
ael ael
12. If NAa =UAa, what do you think can be said about the relationships between
ael
the sets Aa?
13. If J#Ø and JcI, does it follow that U AaSUAq? What about N Aa sN Aa?
aEJ
ael
Ongs to thes
y 0, (Inat
aeJ
ael
only Pa
e have
aEJ
14, If J#Ø and JcI, does it follow that AasN Aa? Explain.
ael
Expert Solution
Step 1
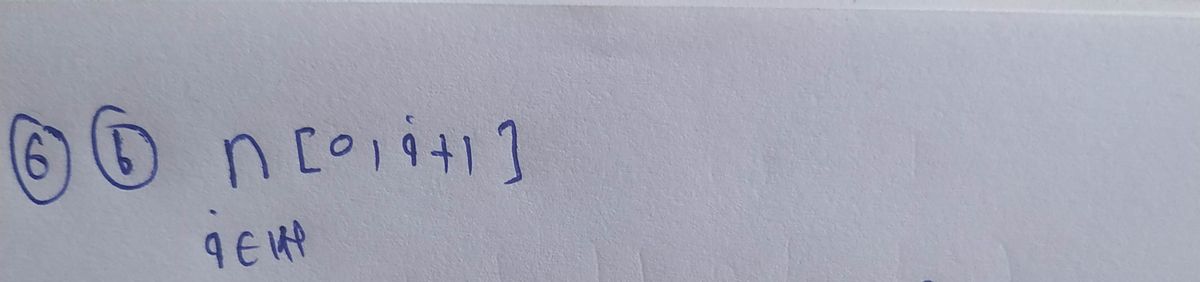
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

