Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Question 29:** Identify the open interval(s) where \( f \) is concave up.
- [A] \((-∞, -1)\)
- [B] \((-∞, -3) \cup (-1, 2)\)
- [C] \((-1, ∞)\)
- [D] \((-2, 1)\)](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F5ef4066a-09c4-44d3-9899-dbf8cf9ac919%2F28218902-96bc-4728-bf4f-a509769d7f15%2Faeakioi_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Question 29:** Identify the open interval(s) where \( f \) is concave up.
- [A] \((-∞, -1)\)
- [B] \((-∞, -3) \cup (-1, 2)\)
- [C] \((-1, ∞)\)
- [D] \((-2, 1)\)

Transcribed Image Text:The image depicts the graph of the derivative of a function, denoted as \( f'(x) \).
### Features of the Graph:
- **Axes**:
- The horizontal axis represents \( x \).
- The vertical axis represents \( f'(x) \).
- **Critical Points**:
- The graph crosses the x-axis at approximately \( x = -2.5 \), \( x = 0 \), and \( x = 2 \). These are points where the derivative is zero, indicating potential local maxima or minima in the original function \( f(x) \).
- **Behavior of the Graph**:
- Starting from the left, the graph has a decreasing trend until just before \( x = -2.5 \).
- After crossing the x-axis at \( x = -2.5 \), the graph increases and then decreases, crossing the x-axis again at \( x = 0 \).
- The graph increases after \( x = 0 \) until just after \( x = 1.5 \), reaching a local maximum.
- Beyond \( x = 2 \), the graph decreases sharply until it extends downward.
- **Arrow Indicators**:
- The arrows at the ends of the graph indicate that the behavior continues in those respective directions beyond the visible portion.
### Interpretation:
- **Increasing Intervals**: The function \( f(x) \) is increasing where \( f'(x) > 0 \). Based on the graph, this occurs approximately between \( -2.5 < x < 0 \) and \( 1.5 < x < 2.5 \).
- **Decreasing Intervals**: The function \( f(x) \) is decreasing where \( f'(x) < 0 \). This is observed for \( x < -2.5 \), between \( 0 < x < 1.5 \), and \( x > 2.5 \).
### Educational Context:
Understanding the graph of the derivative is essential for identifying the behavior of the original function \( f(x) \). This includes recognizing intervals of increase or decrease, and identifying critical points that may correspond to local maxima, minima, or points of inflection in \( f(x) \). This knowledge is fundamental in calculus and helps in sketching and understanding the overall behavior of functions.
Expert Solution
Step 1
for concave up , f'(x) is increasing
For given graph , f'(x) is increasing on
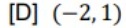
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning