(i) zy' + y = y yº (k) : + yy' = 0 2 x+2 y = V16 – 2 = –
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
please answer j and k

Transcribed Image Text:2. Prove that the functions in the right-hand column below are solutions of the
differential equations in the left-hand columns. (Be sure to state the common
interval for which solution and differential equation make sense.)
(a) y' + y = 0
(b) y' = e
(c)
d²y
dx2
/1
(d) f'(x) = f'(x)
2y
(e) xy'
(f) (1 + x²³)y' = xy
dr
do
(g) cos 0
(h) y"
(i) f'(x)
1
-
2r sin 0 = 0
· y = 0
=
f(x)
x2
(i) xy + y =
= y²
(k) x + yy' = 0
y = e-*.
y = e.
y = x Arc sinx+√1-x².
y = e² + 2.
y =
x².
T =
√1+x².
a sec² 0.
y = ae* + be *.
f(x) = 2e²/3.
2
x + 2
y =√16x².
y =
Expert Solution
Step 1
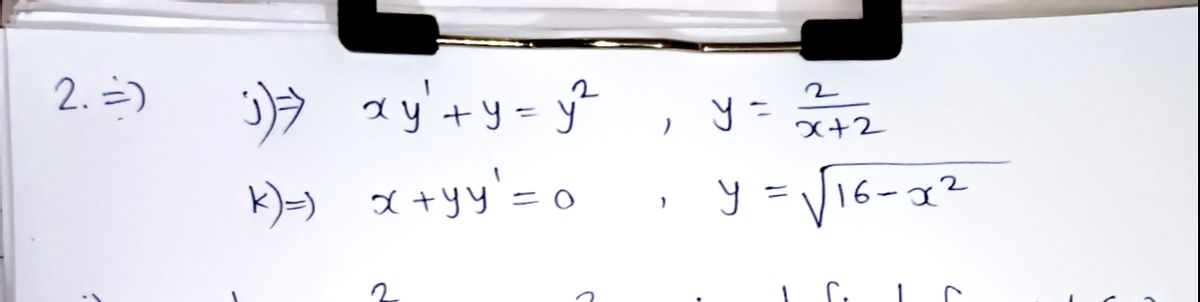
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

