Let A and f(t) be as in Exercise 20. (a) Prove that f(t) = (A₁1-t) (A22-t) (Ann-t)+q(t), where q(t) is a polynomial of degree at most n-2. Hint: Apply mathematical induction to n. (b) Show that tr(A) = (-1)n-¹a an-1.
Let A and f(t) be as in Exercise 20. (a) Prove that f(t) = (A₁1-t) (A22-t) (Ann-t)+q(t), where q(t) is a polynomial of degree at most n-2. Hint: Apply mathematical induction to n. (b) Show that tr(A) = (-1)n-¹a an-1.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Question21

Transcribed Image Text:20. Let A be an n × n matrix with characteristic polynomial
ƒ(t) = (−1)″țn + An-1th-1 +
+ a₁t+ao.
Prove that f(0) = ao = det(A). Deduce that A is invertible if and only
if ao 0.
21. Let A and f(t) be as in Exercise 20.
(a)
Prove that f(t) = (A11 – t)(A22 − t) · · · (Ann −t)+q(t), where q(t)
is a polynomial of degree at most n-2. Hint: Apply mathematical
induction to n.
(b) Show that tr(A) = (−1)n-¹an-1.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
I can't understand the red circle I write.Please explain it in detail.
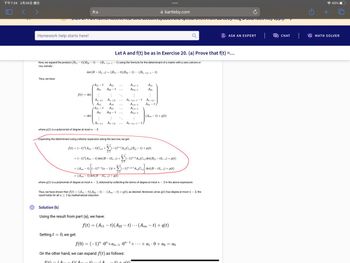
Transcribed Image Text:下午7:34 2月26日 週日
Homework help starts here!
Thus, we have
bartleby.com
NOT FOR TEATS! Receive feat aime accome updates and special offers from paralepy. Mag & data rates may
Now, we expand the product (B₁1 - t) (B22-t) (Bn-1,n-1-
row, namely:
f(t) = det
tiji
= det
=
...
det (B-tIn-1) = (B₁1 – t)(B22 – t) ... (Bn-1,n-1 – t)
A₁1 - t
A21
:
An-1,1
where p(t) is a polynomial of degree at most n - 2.
:
An-1,1
An1
A₁1-t
A21
+)(A
Let A and f(t) be as in Exercise 20. (a) Prove that f(t) =...
A12
A22 - t
t) using the formula for the determinant of a matrix with a zero column or
:
An-1,2
An2
A12
A22 - t
An-1,2
Solution (b)
Using the result from part (a), we have:
Expanding the determinant using cofactor expansion along the last row, we get :
A1,n-1
A2,n-1
An-1,n-1-t
Ann-1
A1,n-1
A2,n-1
n+j
An-1,n-1-t
n-1
f(t) = (-1)" (Ann - t) Cnn +(-1)+ AnjСn,j(Bjj – t) + p(t)
j=1
-
n-1
= (-1)" (Ann – t) det(B − tIn-1) + (−1)n+j AnjCn,j det (Bjj — tIn−1) + p(t)
-
j=1
Ain
A2n
n-1
(Ann – t) (−1)n-¹(n − 1)t + Σ(−1)n+j+¹ AnjCnj det (B − tIn−1) + p(t)
j=1
=
= (Ann- t) det(B − tIn−1) + q(t)
where g(t) is a polynomial of degree at most n - 2, obtained by collecting the terms of degree at most n-2 in the above expression.
An-1,n
Ann -t
(Ann- t) +p(t)
Thus, we have shown that f(t) = (A11 – t) (A22 – t) (Ann- t) + q(t), as desired. Moreover, since q(t) has degree at most n -
result holds for all n ≥ 1 by mathematical induction.
2, the
f(t) = (A11 t) (A22 t) (Ann- t) + g(t)
(+)
Setting t = 0, we get:
= ao
f(0) = (−1)".0″+an-1 .On. +. + a₁.0 + ao
On the other hand, we can expand f(t) as follows:
f(t) (A
+) +
Ć
ASK AN EXPERT
見 CHAT
+
43%
VX MATH SOLVER
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

