Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 miles away.
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experiments to set up the devices.
![### Compound Interest Calculation
**Question:**
How much will you get out from $1000 that grows at 9% compounded monthly at the end of 17 years?
**Explanation:**
To determine the future value of an investment with compound interest, the following mathematical formula is used:
\[ A = P \left(1 + \frac{r}{n}\right)^{nt} \]
Where:
- \( A \) is the amount of money accumulated after n years, including interest.
- \( P \) is the principal amount (the initial amount of money).
- \( r \) is the annual interest rate (decimal).
- \( n \) is the number of times that interest is compounded per year.
- \( t \) is the number of years the money is invested for.
In this case:
- \( P = 1000 \) (the initial amount)
- \( r = 0.09 \) (9% annual interest rate)
- \( n = 12 \) (compounded monthly)
- \( t = 17 \) (investment duration in years)
Substituting the given values into the formula, we get:
\[
A = 1000 \left(1 + \frac{0.09}{12}\right)^{12 \times 17}
\]
### Detailed Calculation:
1. Calculate the monthly interest rate:
\[ \frac{0.09}{12} = 0.0075 \]
2. Calculate the number of times interest is compounded over the period:
\[ 12 \times 17 = 204 \]
3. Substitute and solve:
\[
A = 1000 \left(1 + 0.0075\right)^{204}
\]
\[
A = 1000 \left(1.0075\right)^{204}
\]
Using a calculator for the exponentiation:
\[
A \approx 1000 \times 4.667
\]
\[
A \approx 4667
\]
Hence, at the end of 17 years, you will get approximately $4667 from your investment of $1000 growing at 9% compounded monthly.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F50ecada7-73ae-429a-bfd7-3c03fe93abe4%2F8c9ded0d-0050-48ce-880b-ac11b7f61c4d%2F61b33t_reoriented.jpeg&w=3840&q=75)
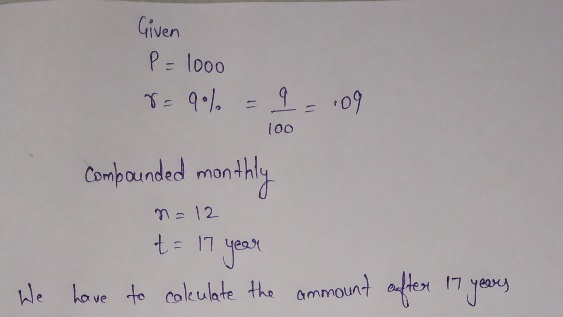
Step by step
Solved in 2 steps with 2 images









