How large should n be to guarantee that the Simpsons Rule approximation to 5 (-z¹ +16x³ - 90x² + 3x + 3) da is accurate to within 0.1. n =
How large should n be to guarantee that the Simpsons Rule approximation to 5 (-z¹ +16x³ - 90x² + 3x + 3) da is accurate to within 0.1. n =
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem Statement:**
How large should \( n \) be to guarantee that the Simpson's Rule approximation to
\[
\int_3^5 \left(-x^4 + 16x^3 - 90x^2 + 3x + 3\right) dx
\]
is accurate to within 0.1.
**Answer:**
\( n = \) [insert value here]
**Explanation:**
This problem involves determining the appropriate number of subintervals, \( n \), required for Simpson's Rule to achieve a specified level of accuracy (within 0.1) for the given integral. The integral function is a polynomial of degree four, given by:
\[
-x^4 + 16x^3 - 90x^2 + 3x + 3
\]
### Simpson's Rule:
Simpson's Rule is a numerical method for approximating the integral of a function over a specified interval. It is especially useful for functions that can be approximated well by parabolas and is formulated as:
\[
\int_a^b f(x) \, dx \approx \frac{b-a}{3n} \left( f(x_0) + 4\sum_{{\text{odd } i}} f(x_i) + 2\sum_{{\text{even } i}} f(x_i) + f(x_n) \right)
\]
where \( x_i = a + i\frac{b-a}{n} \).
### Error Bound:
The error \( E \) in Simpson's Rule is given by:
\[
E = \frac{(b-a)^5}{180n^4} \max |f^{(4)}(x)|
\]
where \( f^{(4)}(x) \) is the fourth derivative of the function \( f(x) \). The goal is to find \( n \) such that \( E < 0.1 \).
After computing the fourth derivative \( f^{(4)}(x) \) and finding its maximum value on the interval \([3, 5]\), we solve for \( n \) to ensure this bound is satisfied.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F5037864c-7b38-4651-b91f-98ef71cc2c30%2F5d5389ed-2cfe-4ca2-86c5-d52c3530c192%2Fst6651_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
How large should \( n \) be to guarantee that the Simpson's Rule approximation to
\[
\int_3^5 \left(-x^4 + 16x^3 - 90x^2 + 3x + 3\right) dx
\]
is accurate to within 0.1.
**Answer:**
\( n = \) [insert value here]
**Explanation:**
This problem involves determining the appropriate number of subintervals, \( n \), required for Simpson's Rule to achieve a specified level of accuracy (within 0.1) for the given integral. The integral function is a polynomial of degree four, given by:
\[
-x^4 + 16x^3 - 90x^2 + 3x + 3
\]
### Simpson's Rule:
Simpson's Rule is a numerical method for approximating the integral of a function over a specified interval. It is especially useful for functions that can be approximated well by parabolas and is formulated as:
\[
\int_a^b f(x) \, dx \approx \frac{b-a}{3n} \left( f(x_0) + 4\sum_{{\text{odd } i}} f(x_i) + 2\sum_{{\text{even } i}} f(x_i) + f(x_n) \right)
\]
where \( x_i = a + i\frac{b-a}{n} \).
### Error Bound:
The error \( E \) in Simpson's Rule is given by:
\[
E = \frac{(b-a)^5}{180n^4} \max |f^{(4)}(x)|
\]
where \( f^{(4)}(x) \) is the fourth derivative of the function \( f(x) \). The goal is to find \( n \) such that \( E < 0.1 \).
After computing the fourth derivative \( f^{(4)}(x) \) and finding its maximum value on the interval \([3, 5]\), we solve for \( n \) to ensure this bound is satisfied.
Expert Solution
Step 1: Determine the given function
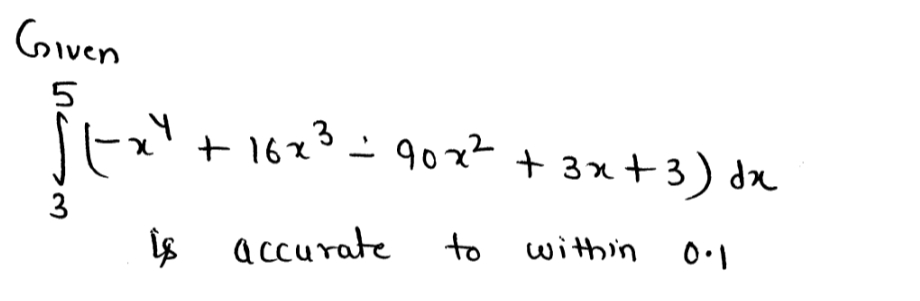
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

