Cost-Volume-Profit Analysis
Cost Volume Profit (CVP) analysis is a cost accounting method that analyses the effect of fluctuating cost and volume on the operating profit. Also known as break-even analysis, CVP determines the break-even point for varying volumes of sales and cost structures. This information helps the managers make economic decisions on a short-term basis. CVP analysis is based on many assumptions. Sales price, variable costs, and fixed costs per unit are assumed to be constant. The analysis also assumes that all units produced are sold and costs get impacted due to changes in activities. All costs incurred by the company like administrative, manufacturing, and selling costs are identified as either fixed or variable.
Marginal Costing
Marginal cost is defined as the change in the total cost which takes place when one additional unit of a product is manufactured. The marginal cost is influenced only by the variations which generally occur in the variable costs because the fixed costs remain the same irrespective of the output produced. The concept of marginal cost is used for product pricing when the customers want the lowest possible price for a certain number of orders. There is no accounting entry for marginal cost and it is only used by the management for taking effective decisions.
How can we determine whether the project under consideration is of normal risk?
Introduction:
Risk is nothing but the variation in real returns obtained as opposed to expected returns in a project. Risk analysis is the method that is often carried out before any project is approved or any investment decision made.
In terms of capital budgeting, with the aid of following strategies we can determine whether a proposal is under normal risk or not:
Net present value (NPV): If the project’s NPV is negative or zero, which means zero or higher, it will be at normal risk.
Standard deviation: The standard deviation is the indicator of return reflection. Therefore the greater the deviation, the greater will be the risk. A project with lower risk should be called normal risk in a comparable scenario. This is calculated by using the formula,
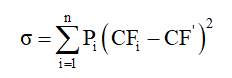
Where, σ is the standard deviation,
P is the probability of occurrence of cash flows,
N is the number of time periods,
CF is the cash flows of the given years,
CF’ is the mean of cash flows
Step by step
Solved in 4 steps with 3 images









