hortest Path Problem Find the shortest path from
Shortest Path Problem
Find the shortest path from a to z using Dijkstra’s

Algorithm:
Both directed and undirected graph
All edge must have non-negative weight
The graph must be clearly connected
Remove all self-loop and parallel edge
It is applied to the weight graph.
STEPS:
The first step of Dijkstra's algorithm is to set all the costs of each vertex that is not original to infinity.
So the cost of b c d e and z are initially set to infinity
And the cost of a is initially set to zero then iteratively which we use the loop.
We will select one vertex that has the lowest cost and includes that vertex into a set of paths
After the vertex is included we will update all the other vertices the cause of all the other vertices.
So it reflects the choice that you make so for the six vertices.
You can see that 'a' has the lowest cost so we initially select a to set when a is selected to the set we have to update neighbors of 'a' which are B and C.
We have to make the cost of vertex should be lower how much lower is that depending upon how much depending upon the existing count.
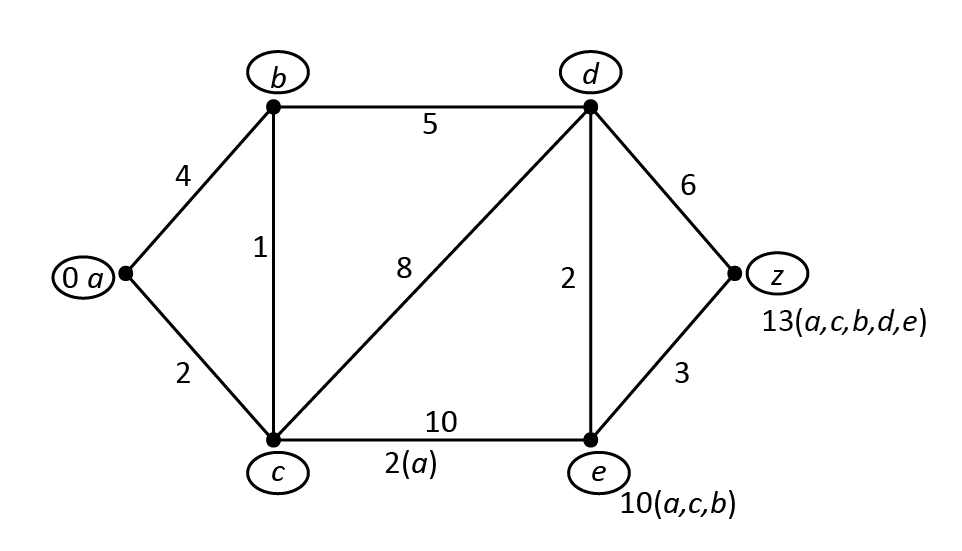
Then the shortest path from a to z is a,c,b,d,e,z with a length of 13
Step by step
Solved in 2 steps with 1 images









