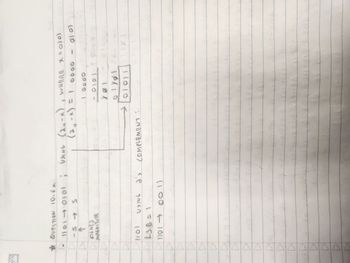Honestly, what does this mean? I'm using 1101 as an example. 1101 is the signed magnitude of 0101. Using the formula (2n - X), I'm getting 10000 and subtracting 0101. After subtracting, I get 01011, but it is not equaling the same as the 2's complement of 1101. How do I solve this question?
Honestly, what does this mean? I'm using 1101 as an example. 1101 is the signed magnitude of 0101. Using the formula (2n - X), I'm getting 10000 and subtracting 0101. After subtracting, I get 01011, but it is not equaling the same as the 2's complement of 1101. How do I solve this question?
Let's start by reviewing what signed magnitude and two's complement representations are:
Signed magnitude: In signed magnitude representation, the leftmost bit represents the sign (0 for positive, 1 for negative) and the remaining bits represent the magnitude of the number. For example, 1101 is -5 in signed magnitude because the leftmost bit is 1 indicating a negative number and the remaining bits represent the magnitude, which is 0101 or 5.
Two's complement: In two's complement representation, the leftmost bit still represents the sign, but the remaining bits represent the magnitude of the number in a slightly different way. To find the two's complement of a number, first take the Boolean complement of each bit (i.e., flip all the 0s to 1s and all the 1s to 0s), and then add 1. For example, to find the two's complement of -5 (represented in signed magnitude as 1101), we first take the Boolean complement of each bit to get 0010, and then add 1 to get 0011, which represents +3 in two's complement.
Step by step
Solved in 2 steps
What am I doing wrong?
by Bartleby Expert
