HBL Bank Pvt LtD. is studying its ATM use in the Gulshan-e-Iqbal area of Karachi. A sample of 30 ATMs showed they were used in the given number of times (in seconds) on a particular day, as shown in Table 1. Identify the presence of outliers in this dataset After removing the outliers (if present) from the given dataset, what is the expected or average number of times (in seconds) the ATM is used in the new dataset (if outliers were detected and removed). Show your results with errors in the statistical expected or average value. 83.24 64.01 84.23 76.20 84.21 54.29 5.11 59.21 70.23 61.01 63.10 80.23 84.21 73.20 68.11 52.19 65.22 90.16 52.16 177.21 95.23 36.15 48.12 16.18 59.32 84.22 195.13 47.18 87.13 26.11
Inverse Normal Distribution
The method used for finding the corresponding z-critical value in a normal distribution using the known probability is said to be an inverse normal distribution. The inverse normal distribution is a continuous probability distribution with a family of two parameters.
Mean, Median, Mode
It is a descriptive summary of a data set. It can be defined by using some of the measures. The central tendencies do not provide information regarding individual data from the dataset. However, they give a summary of the data set. The central tendency or measure of central tendency is a central or typical value for a probability distribution.
Z-Scores
A z-score is a unit of measurement used in statistics to describe the position of a raw score in terms of its distance from the mean, measured with reference to standard deviation from the mean. Z-scores are useful in statistics because they allow comparison between two scores that belong to different normal distributions.
HBL Bank Pvt LtD. is studying its ATM use in the Gulshan-e-Iqbal area of Karachi. A sample of 30 ATMs showed they were used in the given number of times (in seconds) on a particular day, as shown in Table 1.
- Identify the presence of outliers in this dataset
- After removing the outliers (if present) from the given dataset, what is the expected or average number of times (in seconds) the ATM is used in the new dataset (if outliers were detected and removed). Show your results with errors in the statistical expected or average value.
|
83.24 |
64.01 |
84.23 |
76.20 |
84.21 |
54.29 |
5.11 |
59.21 |
70.23 |
61.01 |
|
63.10 |
80.23 |
84.21 |
73.20 |
68.11 |
52.19 |
65.22 |
90.16 |
52.16 |
177.21 |
|
95.23 |
36.15 |
48.12 |
16.18 |
59.32 |
84.22 |
195.13 |
47.18 |
87.13 |
26.11 |
(a)
Identify the outliers from the given data set.
The outliers from the given data set are determined below as follows:
Arrange the given data in the ascending order. The total number of values in the given data set are n=30.
Use EXCEL Procedure to obtain the value of first quartile.
Follow the instruction to obtain the value of first quartile.
- Open EXCEL
- Go to Formula bar.
- In formula bar enter the function as“=QUARTILE”
- Enter the range as $A$1:$A$31.
- Enter the quartile as 1.
- Click enter.
EXCEL output:
From the EXCEL output, the value of the first quartile is 52.715
Thus, the value of the first quartile is 52.715.
Use EXCEL Procedure to obtain the value of second quartile.
Follow the instruction to obtain the value of second quartile.
- Open EXCEL
- Go to Formula bar.
- In formula bar enter the function as“=QUARTILE”
- Enter the range as $A$1:$A$31.
- Enter the quartile as 2.
- Click enter.
EXCEL output:
From the EXCEL output, the value of the second quartile is 66.665.
Thus, the value of the second quartile is 66.665.
Use EXCEL Procedure to obtain the value of third quartile.
Follow the instruction to obtain the value of third quartile.
- Open EXCEL
- Go to Formula bar.
- In formula bar enter the function as“=QUARTILE”
- Enter the range as $A$1:$A$31.
- Enter the quartile as 3.
- Click enter.
EXCEL output:
From the EXCEL output, the value of the third quartile is 84.21
Thus, the value of the third quartile is 84.21.
Obtain the value of the Inter quartile range.
The value of Inter quartile range is obtained below:
The formula to obtain IQR is,
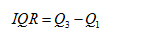
Where Q3 denotes the third quartile.
Q1 denotes the First quartile.
The required value is,
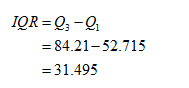
Thus, the value of Inter quartile range is 31.495.
Identify the outliers.
Rule for outliers:

It is clear that if any data point falls outside the interval (5.47,131.45) are considered as outliers.
There are three data points considered as outliers that falls outside the interval are 5.11, 177.21 and 195.13.
Step by step
Solved in 2 steps with 3 images




